
So far we were showing that it is possible to improve Kalman filter estimations simply by adding a second observer for the same system state. Now we will expose how to fuse noisy measurements from different sources into a single measurement and in which way the noise can be efficiently reduced.
Literature:
- Fehlerausgleichsrechnung (German site)
- Fehlerrechnung (also in Gernan)
- The Kalman filter (Prof. Paul Rojas, Freie Universitšt Berlin)
Suppose that we have two statistically independent measurement sources Z1 and Z2 with the respective noise variances R1 and R2 that try to determine the state of our system x. Again we assume that the noise is white and Gaussian and that it has zero mean. Example: We have two voltmeters that measure the same voltage and return 4.8V and 5.4V. The standard deviations are 0.5V and 1.2V, equivalent to the variances 0.25 and 1.44. Without repeating the measurements, how can we optimally fuse these measurements, in order to get a best estimation of the real voltage? How do we solve such an everyday problem - you have two watches showing different times - ? Normally we would choose the "best-case-plus-worst-case-divided-by-two" solution, considering one of both measurements as the best and the other as the worst, then just average. In this case we would obtain a mean of 5.1V. But is this the best estimation? And, what can we say about the standard deviation or the variance?
The best fusion of the measurement data can be developed similarly to the calculation of the optimal Kalman averaging of the a priori estimation and the measurement (Chapter 3):
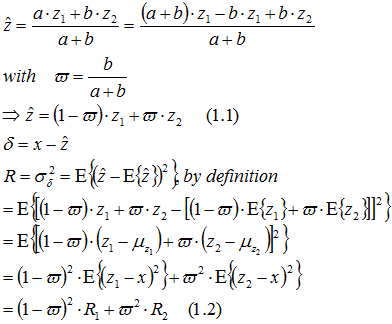
If the fused variance R is considered as a function of the weighting factor, it can be minimized with:
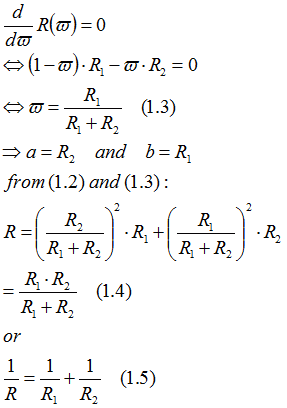
Equation (1.4) forms the harmonic mean of the initial variances.
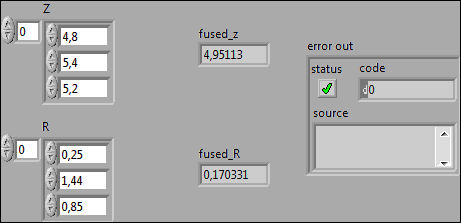
If we come back to our example of the voltage-measurements, we get:
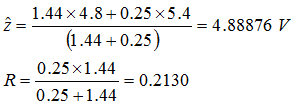
2. Fusing more data sources
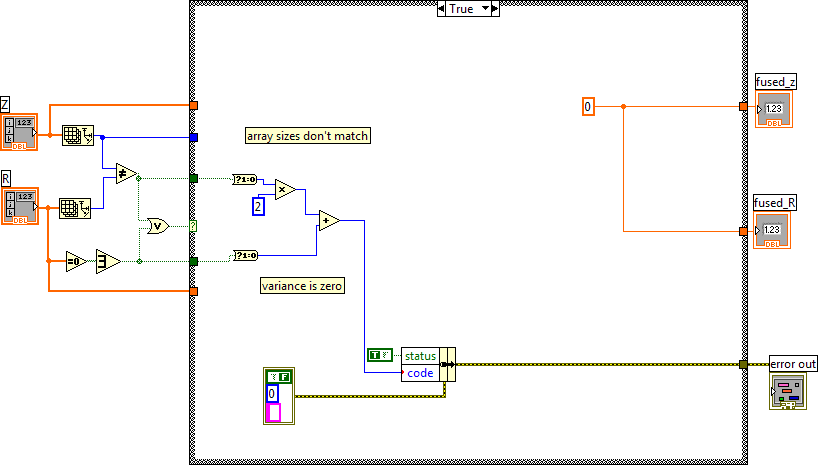
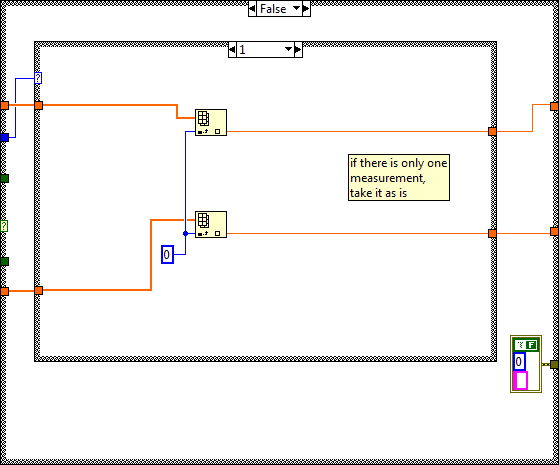
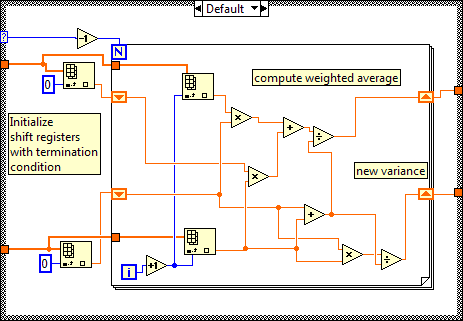
The optimizing procedure may easily be applied to more measurement sources. Probably the most efficient way is to use the following recursive function that is based on the assumption that successive minimization of the measurement noise, through optimal averaging, results in the overall noise minimum and by consequence in the optimal fusing of the measurements. Although this recursive function is not easy manageable in manual calculations, it is very efficient on a computer:
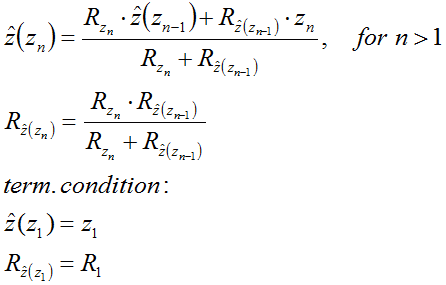
Example: A third multi-meter measures the voltage from the previous chapter as 5.2V with variance 0.85.
The fused estimate then is:
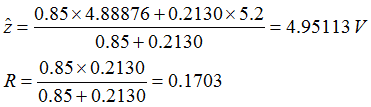
We implemented this recursive function into a LabVIEW (version >=8.2) program: download fuse_measurements.vi (part of an online growing library Kalman_filter.llb).
- Note that the order of the measurements (and of course the corresponding variances) may be inverted
- Errors are produced
- if the number of measurements and the number of variances are unequal
- if one of the variances is zero