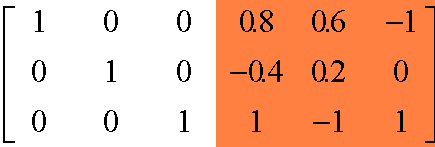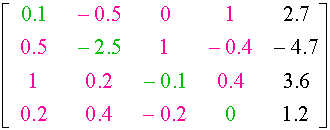
Gauss-Jordan Elimination
We got several e-mails around the polynomial data-reduction technique. We explain here the Gauss-Jordan algorithm for those who wish to understand solving a system of simultaneous equations. Of course there are other methods, but this one is known to be quick, easy to understand and flexible. It is much simpler than the more familiar techniques following algebraic substitution or the use of determinants.
Example:
Solve the following system of simultaneous linear equations:
0.1 x1 - 0.5 x2 + x4 = 2.7
0.5 x1 - 2.5 x2 + x3 - 0.4 x4 = -4.7
x1 + 0.2 x2 - 0.1 x3 + 0.4 x4 = 3.6
0.2 x1 + 0.4 x2 - 0.2 x3 = 1.2
All the factors are written into a matrix :
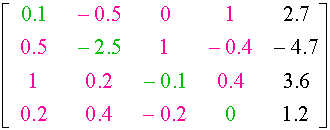
The idea is to transform this array, row by row, until the first four (coloured) columns become zero except the elements on the principal diagonal. At the end, the last column will contain the values of the unknown x's :
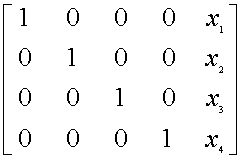
Each transformation consists in adding some multiple of one row to another row, in such a manner that the desired result 1 or 0 is obtained.
Procedure:
1. Transform the first column to (1,0,0,0) through :
multiply the first row by -5 = - a12 / a11 and add to the second row.
multiply the first row by -10 = - a13 / a11 and add to the third row.
multiply the first row by -2 = - a14 / a11 and add to the fourth row.
multiply the first row by 10 = 1 / a11.
As you noticed a11 (and all the elements of the principal diagonal) may not be equal to 0. If this situation is given, the zero must be removed from the principal diagonal by interchanging rows. We get :
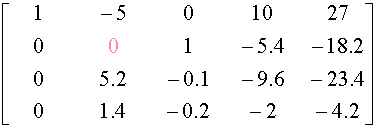
2. Remove the zero from the principal diagonal by interchanging the second and the third rows (or the second and the fourth). The result is :
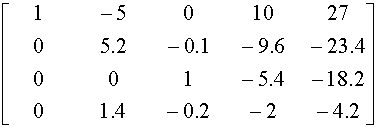
3. Transform the second column to (0,1,0,0) as follows :
multiply the new second row by 5/5.2 = 0.962 = - a21 / a22 and add to the first row.
the third element of the target-column is already a 0, so there mustn't be done anything.
multiply the second row by -1.4/5.2 = -0.269 = - a24 / a22 and add to the last row.
multiply the second row by 1/5.2 = 0.192 = 1 / a22
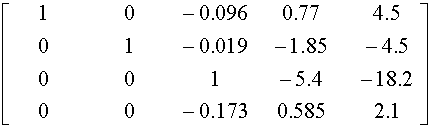
4. Transform the third column to (0,0,1,0) by :
multiply the third row by 0.096 and add to the first row.
multiply the third row by 0.019 and add to the second row.
multiply the third row by 0.1273 and add to the fourth row.
the third element of the principal diagonal is already a 1, so there is no change.
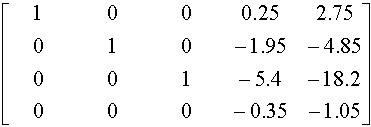
5. Transform the fourth column to (0,0,0,1) with :
multiply the fourth row by 0.25/0.35 = 0.714 and add to the first row.
mutiply the fourth row by -1.95/0.35 = -5.571 and add to the second row.
multiply the fourth row by -5.4/0.35 = -15.429 and add to the third row.
multiply the fourth row by -1/0.35 = -2.86
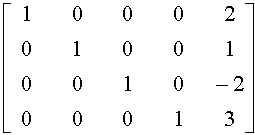
Note: If the determinant is zero, there is no solution to the system.
DOWNLOAD a Robolab 2.5 / Labview 6 program.
Note: if you build an array of the form :
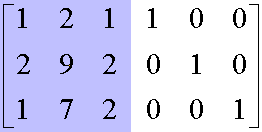
and operate on it the Gauss-Jordan Elimination, you obtain the following matrix, where the second part is the INVERSE MATRIX of the blue part above :