Data-reduction using the Least square polynomial
Sometimes you have to operate on a more or less large set of data. Manipulating such sets is generally difficult.
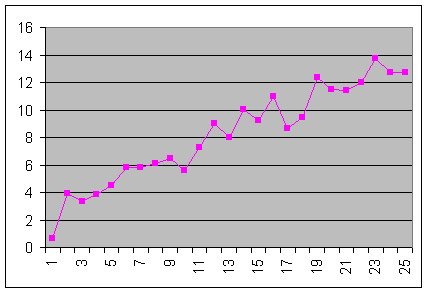
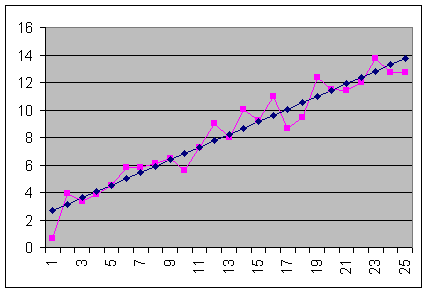
Suppose your result should be a straight line in a plane area, but of course your data only moves around. You guess that there is a linear tendency, but the computer doesn't. Here the example of a 25 data-set:
| x | y | x2 | xy |
| 1 | 0,66496424 | 1 | 0,66496424 |
| 2 | 3,94075718 | 4 | 7,88151436 |
| 3 | 3,35247829 | 9 | 10,0574349 |
| 4 | 3,86552513 | 16 | 15,4621005 |
| 5 | 4,49854689 | 25 | 22,4927345 |
| 6 | 5,80525828 | 36 | 34,8315497 |
| 7 | 5,81779177 | 49 | 40,7245424 |
| 8 | 6,10924665 | 64 | 48,8739732 |
| 9 | 6,48756951 | 81 | 58,3881256 |
| 10 | 5,59638624 | 100 | 55,9638624 |
| 11 | 7,28547502 | 121 | 80,1402252 |
| 12 | 9,0264179 | 144 | 108,317015 |
| 13 | 8,02644055 | 169 | 104,343727 |
| 14 | 10,0489198 | 196 | 140,684877 |
| 15 | 9,21802309 | 225 | 138,270346 |
| 16 | 10,9809859 | 256 | 175,695774 |
| 17 | 8,63910735 | 289 | 146,864825 |
| 18 | 9,44954277 | 324 | 170,09177 |
| 19 | 12,3358053 | 361 | 234,380301 |
| 20 | 11,5203612 | 400 | 230,407224 |
| 21 | 11,4433213 | 441 | 240,309747 |
| 22 | 12,0350019 | 484 | 264,770042 |
| 23 | 13,729675 | 529 | 315,782525 |
| 24 | 12,7141765 | 576 | 305,140236 |
| 25 | 12,7032674 | 625 | 317,581685 |
| 325 | 205,295045 | 5525 | 3268,12112 |

Suppose you have N data points (xi, yi). The equation for the straight line is y = c1 + c2x, where c1 and c2 are unknown.
The error of the real yi-value compared to the straight line is declared as ei = yi - (c1 + c2x)
To make sure big errors have a more important impact on the computation, we consider the sum of the squared errors:
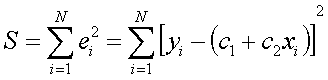
As we want to find the values c1 and c2 that will make sure S will be minimized, we set the partial derivates of S respective to c1 and c2 equal to zero:
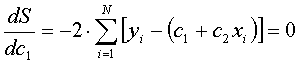
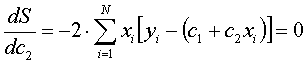
Rearranging these equations we get:
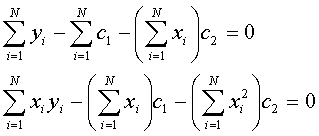
Again rearranging we have:
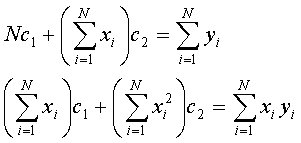
To extract c1 and c2 we must only solve the system of two simultaneous equations.
Our example:
25c1 + 325c2 = 205.295045
325c1 + 5525c2 = 3268.12112
Using the determinant-procedure we get:

This technic may be generalyzed as:
y = c1 + c2x + c2x2 + ... + cm+1xm+1
if m=1 we fit the data in a straight line, if m=2 it is a parabola...
The coefficients are determined by solving the m+1 simultaneous equations:
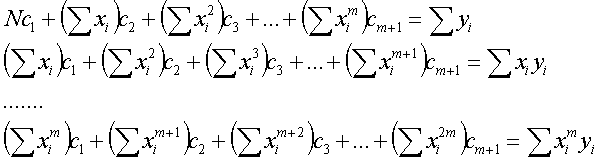
Of course solving more simutaneous equations requires an adequate algorithm such as the Gauss-Jordan Elimination.