Journal       

created 2008/03/16   last update 2010/01/28

==> NEW Kalman Filter with indoor GPS
some links:

2008/03/16 

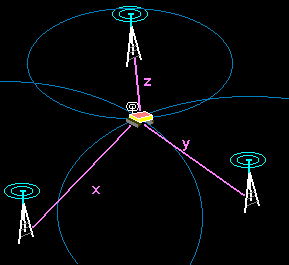
It was time to bring one of our most ambitious projects to the NXT level. We remind the main idea, which is to have a GPS-like system composed of several beacons that send out infrared signals together with ultrasonic bursts. The infrared flash of a single beacon almost arrives instantaneously at the robot that is equipped with a combined infrared/ultrasonic receiver. But the ultrasonic signal only arrives with a certain delay, due to the "slow" sound velocity, in comparison to the speed of light. The receiver is able to measure the time lag between both signals and deduce the distance between the robot and the beacon.

The main issues with the previous devices were:

 

    • accuracy was limited to about 4cm
    • multi-robot applications weren't possible
    • neither the IR-sender nor the ultrasonic transmitter were optimal in terms of power efficiency, with the result that the system was too much directionally sensitive and thus could not be used in larger rooms
    • synchronization between the beacons was too difficult and needed several RCXs

GENERAL DESCRIPTION OF THE NEW SYSTEM:

    • indoor robot navigation
    • allows multi-robot localization
    • error less than 1cm
    • low current dissipation
    • tested over a range of 10 meters

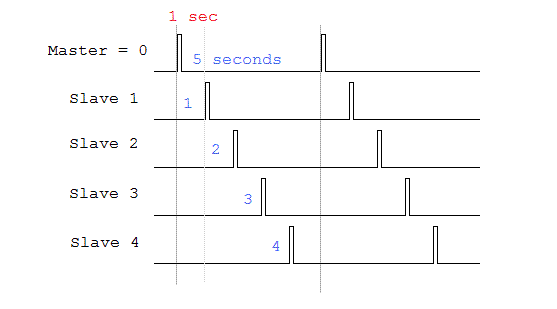
1. BEACONS

    • participation of up to 7 beacons that may be placed at strategically interesting places
    • the beacons send out strong IR and ultrasonic signals that don't require reflectors on the receiver side
    • like RF-beacons, these beacons transmit their identification number, making localization easy
    • always one beacon acts as the master beacon, sending out a synchronization message to all other slave beacons
    • the master beacon with system ID=0 transmits out a standard RCX compatible IR 0xF7 message. The lower nibble of the message-value is Master_ID# = 0. The higher nibble is the number of participating slaves N_s. (Example: If there are 4 slaves, the message-value will be 0x40.) Note that the beacon doesn't expect any reply on 0xF7 messages, as it also is the case with the RCX.
    • After successful transmission of the IR-message, the master-beacon sends out a short ultrasonic burst of 1.25ms duration at 40kHz. Now the master waits (N_s+1) seconds before restarting the procedure.
    • Then the system waits exactly 1 second, after which the first slave sends out its 0xF7 IR-message. The message-value now is Slave_ID# = 1. After correct IR-transmission, the slave produces a short ultrasonic burst.
    • The beacons are jumper configurable. (One jumper defines whether the device acts as the master, the other three jumpers set the Slave_ID# or in the case of the master the number of participating slaves N_s.)
    • Each beacon is equipped with an infrared receiver (obsolete in the case of the master). If the slaves receive a master-message (with low nibble 0 and high nibble <>0), the slave calculates its wait-time before being able to resend the signals. (Slave1 must wait 1 second, Slave2 waits 2 seconds and so on.). This procedure guarantees that the master beacon synchronizes the whole system. (The pause between sending, now being 1 second, could be reduced in a future firmware with a lowest limit of 35ms needed for sending the 0xF7 message composed of 9 bytes plus the ultrasonic burst.) 

2. RECEIVERS

    • Any participating robot must be equipped with a receiver. There is no limit for the number of receivers, because the receiver-devices do not interact.
    • The receiver is NXT-compatible. It is powered from the NXT and is configured as aa I2C-slave, answering to NXT requests.
    • If a receiver gets an infrared identification number message from on of the beacons, a timer is started. It is stopped, once the ultrasonic burst has been received too, or if a timeout occurred (after about 56ms). The minimum detectable delay is 0.87 microseconds, which is due to the oscillator clock 18.432MHz and the timer pre-scale of 1:4, one cycle being 4 clock pulses. This delay corresponds to a path-length of the ultrasonic signal of x=c*t =343*0.87E-6=0.3mm, assuming that the sound velocity at ambient temperature is 343m/s. The firmware uses a 16bit timer that under the given configuration produces an overflow after 56.88ms, corresponding to a distance of 20m.
    • The receiver stores a long message at each measurement event (data-struct see below), composed at this point of the development of non-changeable system information and beacon data.
    • I2C requests from the NXT force the device to return the beacon-data to the NXT-module. Device address is 0x40. The device sends multi-bytes, among which a valid-data-state value, indicating, whether the current data is (or is not) being changed by a new measurement. Further the current device-time of the measurement and the distance in cm (two bytes big endian). The beacon-data packet is completed by a checksum.

In the actual firmware only the beacon data is available

  • The beacon_ID#0 data-struct starts at address 0x9 (8 bytes). All other beacon data are at 0x9+8*ID#.

 

3. NXTs

    • the NXT equipped robots should know the positions of the various beacons
    • for slow motion robots the current position can be deduced by trilateralization
    • fast moving robots need additional dead-reckoning methods fed into a Kalman filter in order to find a best estimate of the position.
    • NXTs must provide the 4.3V AND the 9V power-supply for the receiver-device. The data is asynchronously retrieved through I2C.

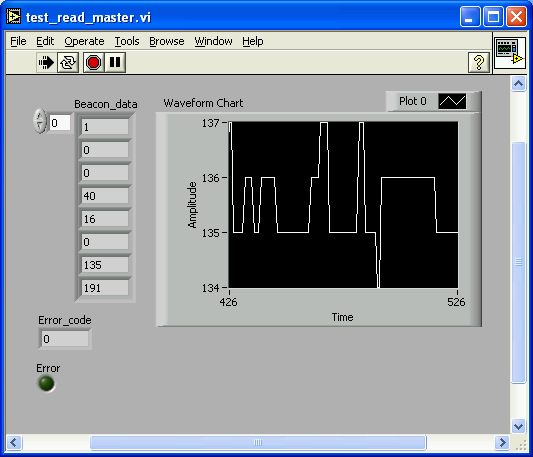
Here a simple ROBOLAB 2.9.4 program that fetches the beacon_ID#0 data from the receiver and displays the results:

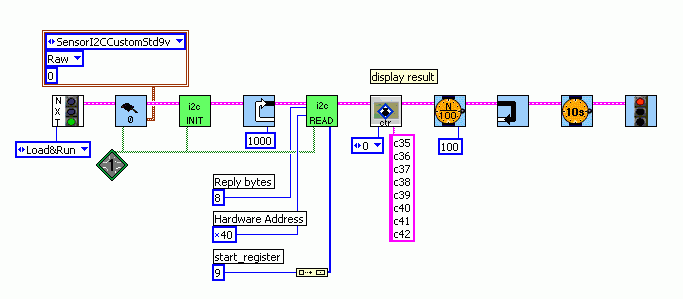
Thanks Chris Rogers for the hints. (I2C sub.vis may be found in ..\ROBOLAB29\vi.lib\Swan\Swan.llb)

With the LabVIEW toolkit, we get the following results:

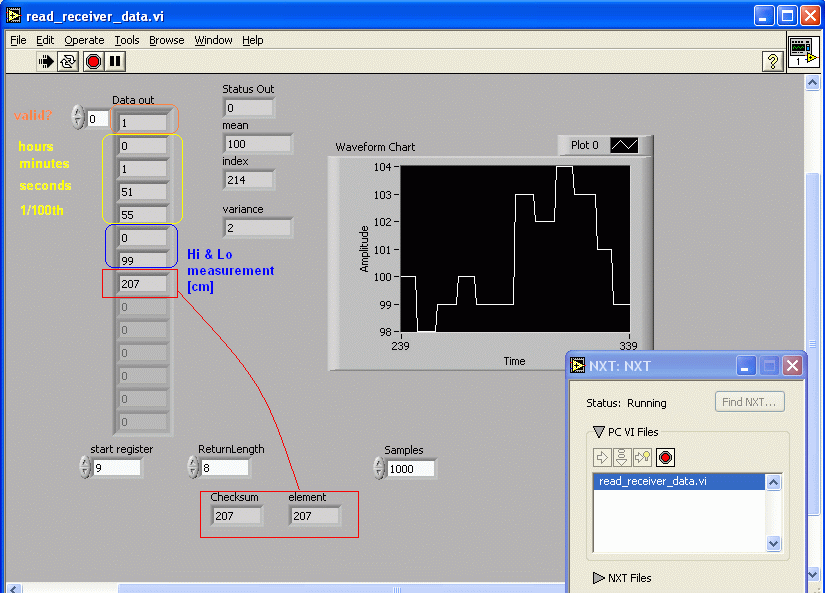
Note that, at this point of the development, the time stamp only indicates the time since the start of the receiver.

4. Test-results:

The first tests with the device show the following results:

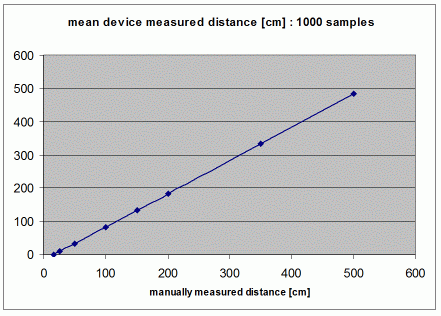
Notes : 

  • For test reasons, the 16bit timer value that determines the measured distance in maximal 65535 steps of 0.3mm is converted into cm, with an obvious loss of information.

  • These first tests do not distinguish constant errors that are due to the constant offset of the ultrasonic detector, from spurious errors.

  • Future firmware will return the raw 16bit timer value that the NXT can convert into distance through x=c*t.In order to get even more precision, the user could add a temperature sensor that might help fixing the thermo-variable sound velocity.

5. Schematics

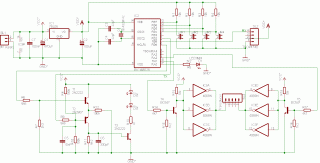
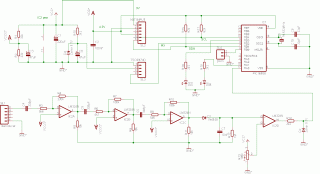
Characteristics:

    • beacon jumpers :  XXX Y, where XXX = ID# number (or, in the case of the master beacon number of slaves N_s); Y = Master (set); Slave (cleared)

    • beacon IR-sender: transistors T1/T2 work as a digital AND-function. If the TX line goes LOW, T2 is conducting and the carrier signal switches T3 via T1 powering the IR-LEDs. The circuit assures 100mA fwd current through the LEDs, producing a very high infrared light intensity. The carrier-signal is generated through the PIC16F628 PWM module.

    • beacon ultrasonic sender: the 2x3 IC3 4069N drivers allow sufficiently strong currents through the ultrasonic transducer that oscillate between -16mA and +16mA , thus generating a high ultrasonic signal strength. The oscillation at 40kHz is generated through alternating HIGH/LOW states of PIC16F628 RA1/RA2.

    • The receiver ultrasonic amplifier has high gain, with a significant maximum at 40kHz. The following signal detector has reaction speed less than 40 microseconds. This delay produces an offset that should be taken into account in the evaluation of the distance measurement.

    • The sensitivity of the comparator should be regulated to produce best reaction in the presence of 40kHz ultrasonic signals. Since the sensitivity voltage is proportional to the battery voltage that directly powers the amplifier, the comparator will react similarly at any battery level. (Regulation of the sensitivity should be done with the volt-meter applied to the output of the comparator.

    • Note : The receiver PWM output does not work in the present firmware.

Last minute changes:

    • Laurent Kneip suggests that beacon transistor T3 should be added a 200Ohm resistor between collector of T2 and base of T3, in order to prevent too high BE-current.

    • In the realized beacon circuit, PIC16F628 pin RB3 produces the 38kHz infrared carrier instead of RB0 (not changed on the schematics yet.)

    • In the realized receiver firmware, the IR and ultrasonic red LEDs have been exchanged inadvertedly (correct on the PCboard-photo below)

    • added on 2008/03/18 : when sending IR-signals, there is a voltage drop that is sufficient to trigger the infared receiver on the beacon circuitry. We therefore added a 100nF capacitor directly soldered between the power-supply pins of the TSOP1738. (neither indicated on the schematics nor visisble on the photo.)

    • the schematics indicates TSOP1740, which is wrong.

6. PC-boards

7. PIC firmware

The firmware has been realized with ULTIMATE for PICs.

  • BEACON: 16F628; Note that the main configuration bits should be changed to set the PWM to RB3 !!! download .asm  .hex

    • The firmware starts with a self-test function:

      • if the beacon is configured as a slave, its ID# number may not be zero, which reserved for the master. In that case, the firmware enters an error-state (a fast flashing red LED). The error-state can only be exited by disconnecting the battery and forcing a restart of the firmware with correct configuration

      • if all went well so far the red LED flashes ID# number of times.

      • now the ultrasonic transducer produces a 2 seconds weakly audible signal

      • after which the continuous beacon procedure is started as described above

  • RECEIVER: 16F88 download .asm  .hex

    • This firmware shortly flashes the ultrasonic LED signal indicator.

    • Then the normal receiver function is started

    • If an IR-signal is received, the red IR LED indicator flashes. Only then, if the expected ultrasonic signal is received, the ultrasonic signal flashes.

    • ADDONS 20/02/2009 : The receiver communicates with the NXT via I2C. The PIC16F88 is configured as a slave and allows reliable multi-byte transmission.

2009/01/24

8. addons

  • We got our copy of Michael Gasperi's book "LabVIEW for LEGO Mindstorms NXT". Great job Mike! So, it was time to start playing with the toolkit again.

  • Since this project was still on the workbench, it seemed to be the very first to get the input from the book.

Updates from the former version (cf. point 3 above):

  • Download LV7.1 NXT toolkit code

  • Much simpler code; consequent use of the sequence wire; creation of sub.vis

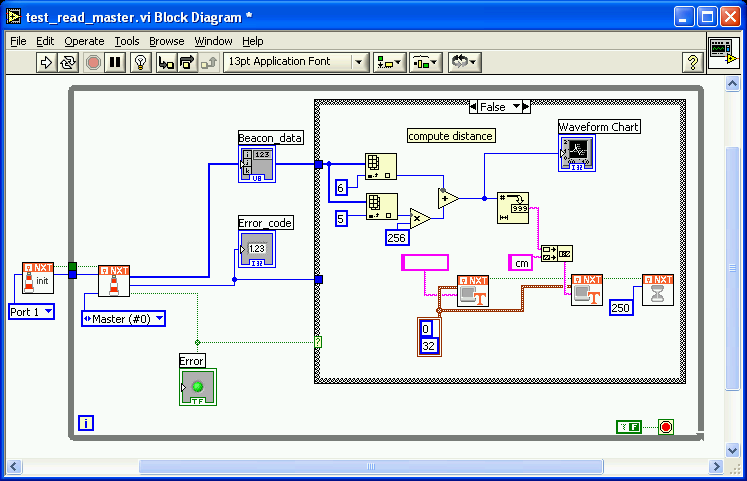
  • We added error messages for the three main error states:

    • 0: no error

    • 1: I2C error

    • 2: array size doesn't match

    • 4: checksum error

    • other odd values represent logical combinations of these errors: example error 5 = 1+4=I2Cerror & checksum error

  • For some reason the PIC firmware does not add the very first "1" (denoted "valid") to the data-checksum computation. This probably caused some headache to those who tried to rebuild the system. Sorry for that. In the NXT toolkit program, the first array-field therefore isn't counted either (which also was done above, but we forgot to mention it!!)

  • There is a nasty bug that needed a long time to be fixed: in earlier tries, if an error occurred, the program just stopped with the mention on the NXT display: "file error". The reason for it was that through the program we are using dynamic data-arrays that may have zero size in the case of an error. If then we attempt to read at any index, the NXT traps in a fatal error state and stops the program. There is no warning or error message in LabVIEW for this event, neither during design-time nor debugging time. (NI guys, consider adding that error message on the PC-screen!!!) We are pretty sure that non-experienced users will seek during extremely long time and desperate here. Mike, could you add a note on your web-site as a complementary instruction to your book?

 

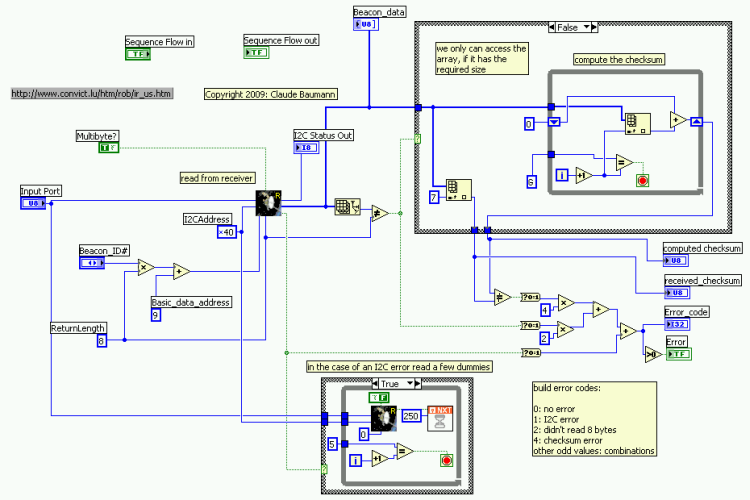
2009/03/25

9.   1D-navigation with a scalar Kalman filter

The infrared-ultrasonic beacon-system represents a real global positioning system. Navigating a robot with such a system is as difficult as using a real GPS. The main issue that we already dealt with while developing our soccer projects -where we used the LEGO camera as global positioning system- is that we receive the GPS-data with a certain delay and at uncertain moments. Normal averaging methods can retrace the robot path, but cannot control it, because they don't tell us the actual position. Here now for the very first time, we are using a scalar Kalman filter for driving a robot on a straight line, where we want the robot to follow a 1D-trajectory. This means that the robot should meet certain target-points at precise moments.

The beacon system uses the Master-beacon alone with the receiver. But we configure the Master so that it thinks there was another Slave beacon. By this way, we only send a new update every second. By comparing the received time stamps and verifying GPS-errors (let's denote the system as such), the NXT deduces whether there is a valid update. The data is fed into a scalar Kalman filter that we wrote entirely in the LabVIEW toolkit -no matrices were necessary-. The Kalman filter essentially predicts the robot's position from the sensor data and its internal model of the motion-system. It then compares the prediction with the new sensor-values and adjust the statistics of the positioning-processes and readings. Finally the prediction is corrected to form the very best estimate of the robot's position along the straight line.

The motors are controlled from the differences that are noticed between the different target-points and the estimated positions.

The program logs the data into a text file from which we extract the results. DOWNLOAD PROGRAM.

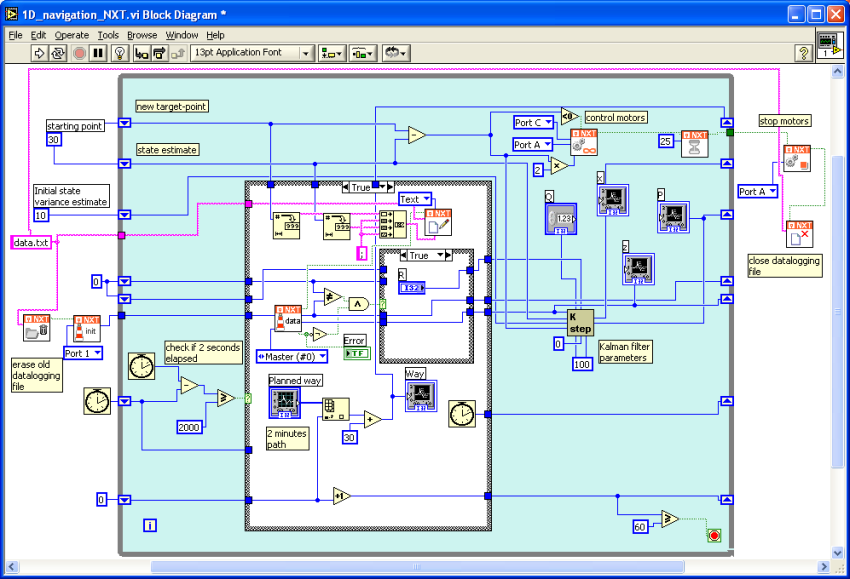
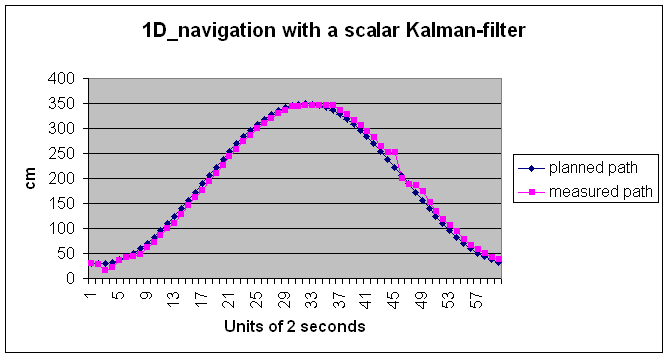
  • Notes:

    • As usual for any Kalman filter, the very first values may diverge from the real values, but they rapidly converge, as can be seen on the picture.

    • In this particular case, since the filter must obey a planned path, the measured path must follow with a short delay

    • Depending on the filter parameters, the Kalman filter has a more or less rapid response to changes or even errors in the measurement. An error occurred at unit 45 causing the filter to react strongly by increasing the robot's speed.

2009/04/18

10. The PIC firmware details  

As explained above, the system combines a set of beacons with a NXT compatible receiver. The devices are driven by PIC 16F628 and 16F88 respectively. We have been asked, if we could publish the source code. As it is written in Ultimate for PICs, it represents a graphical code that may be easily understood as a kind of flow-chart programs.

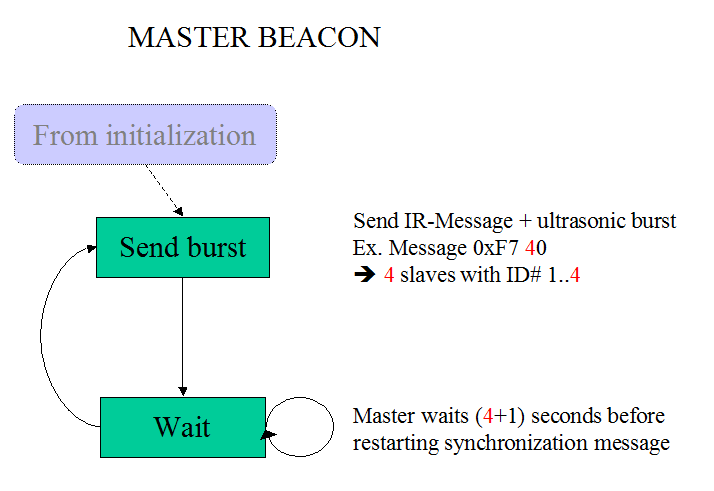
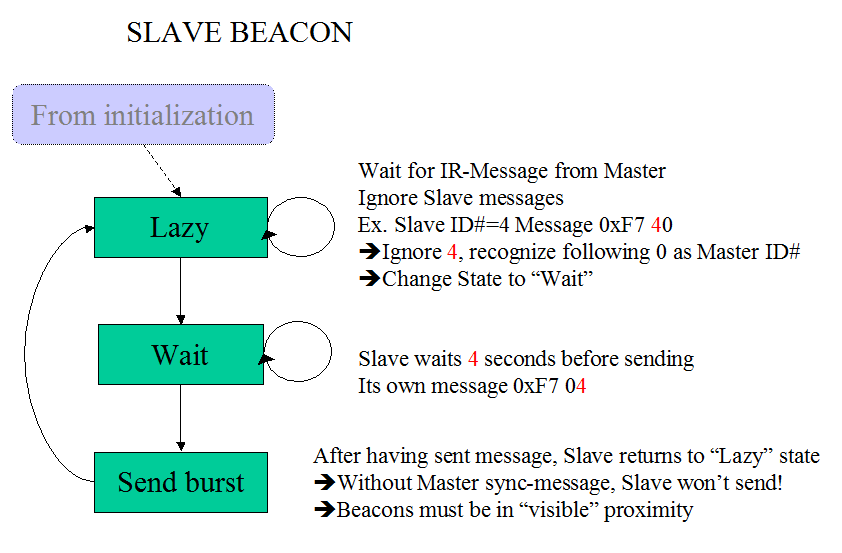
Links:

For better comprehension we add the beacons' state machines hereby.

  • Note that the infrared receiving for the beacons and the receiver works in interrupt mode. This means that as soon as a new serial byte is received, the ISR (interrupt service routine) immediately checks, whether the byte is valid, e.a. that it corresponds to the expected byte. Since the IR channel uses the very robust standard LEGO RCX protocol, each message has a fixed header 0x 55 FF 00, followed by the fixed message code and its complement 0x F7 08. Only then follows the message byte and its complement and the packet checksum plus complement. If at any time the expected byte is missing, the infrared RX channel is reset.

  • The infrared channel is configured 2400 odd 1. Note that the RX channel does not verify the parity, although the 9th bit is configured. (The parity bit only has been added to complete the LEGO RCX message, if ever it was desired to verify the message sending by the beacons easily without other additional hardware than the standard RCX. (Interesting link about the RCX serial configuration: http://www.robotika.sk/mains.php?page=/projects/rcxbt/ )

  • The beacons also need the serial TX channel, which is used in back-to-back mode. After the first filling of the TX-output buffer, the TX interrupt is activated. At each interrupt, the buffer is refilled with the next byte, until all have passed. When the first byte is send, the 38kHz infrared carrier is activated (in PWM mode). The carrier only is stopped -and the serial TX interrupt, after two dummy bytes have been filled in the TX, because the otherwise the last two bytes in the PIC hardware buffer would not be covered by the carrier signal. This causes a delay of 2x9x417us=7.5ms (2 bytes, 9 bits, 1/2400 duration per bit) before the ultrasonic burst is sent.

  • ==> Therefore the receiver will be not be able to measure distances to any beacon below 7.5E-3*343=25.5cm !!! (speed of sound c=343m/sec)

  • The receiver I2C channel is configured in "Slave" mode. The NXT should provide the Master pulse. Since we learned that the bit-banged NXT I2C master sometimes gets lost in waiting for a certain ACK that might never come, we decided to verify every 1/100th second, if the state of the I2C channel is hooked somewhere. If it is longer than 5 seconds in the same state, the whole communication modules (also the UART) are reconfigured. This important measure helped reducing the errors to almost zero, even with multi-byte messages.

  • Some minor features still are not implemented.

 

2009/10/22

11. Localizing a NXT robot in 2D with the iGPS  

This took quite a long time for the journal to awake. But, here we are again.

NEW:

  • We finally builded a second beacon, etched the PC-board, soldered the parts, plugged the battery... and without any trouble it immediately worked.

  • The beacon wait-time has been reduced to 250ms instead of 1sec.

  • ==> Now we will be able to navigate in the plane with our robot

  • We rename the whole system iGPS (= indoor Global Positioning System)

  • Recall that two beacons are sufficient to navigate in a determined half-plane (the beacon line must then be one of the main axis.)

    • iGPS allows multirobot application, because receivers don't intervene in sending infrared or ultrasonic bursts

    • If the beacons are placed almost in the same plane than the receiver, we recommend adding a reflector to the ultrasonic receiver. (Unfortunately the IR-receiver is shadowed, but this doesn't matter, because the IR-pulses are so striong. We used the LEGO part that LDraw denotes "Dish 8x8 Inverted" (see next picture) and drilled a hole in the middle.

  • The NXT now is programmed with LabVIEW Education Edition (LVEE)

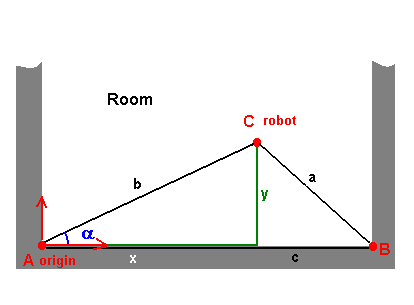
We are able to localize the robot in the plane by applying the cosinus theorem. Note that in the very first test, we deliberately ignore that the beacons height.

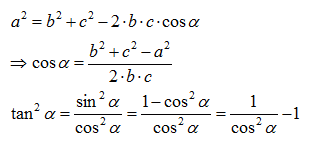
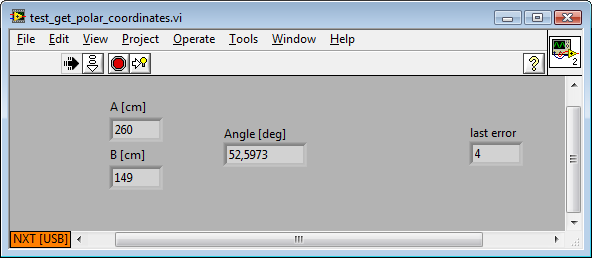
We manually measure 54°.

And the NXT yields the robot polar coordinates C(52.6°, 149cm):

Here all the LVEE codes:

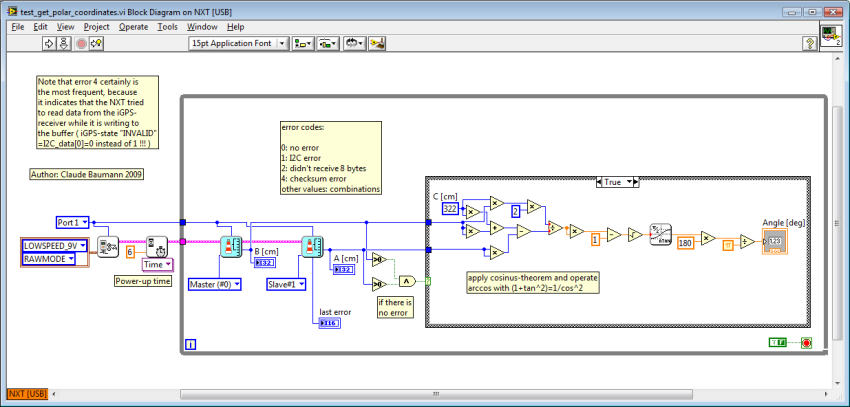
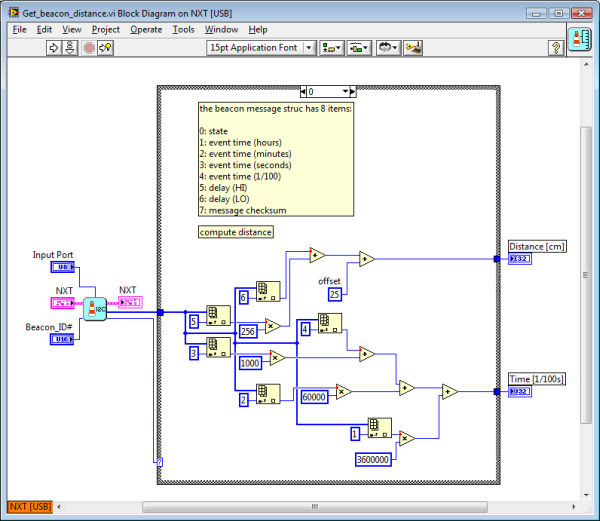
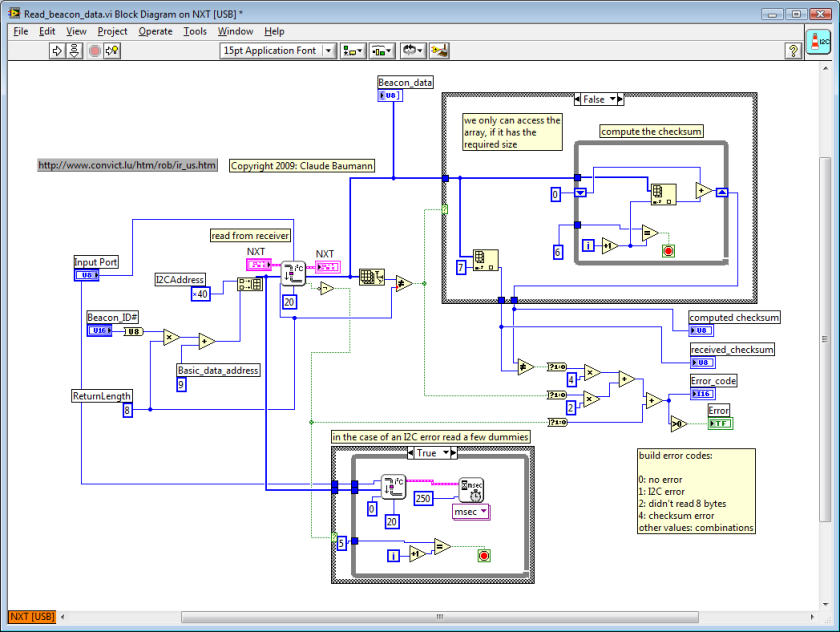
2009/10/23

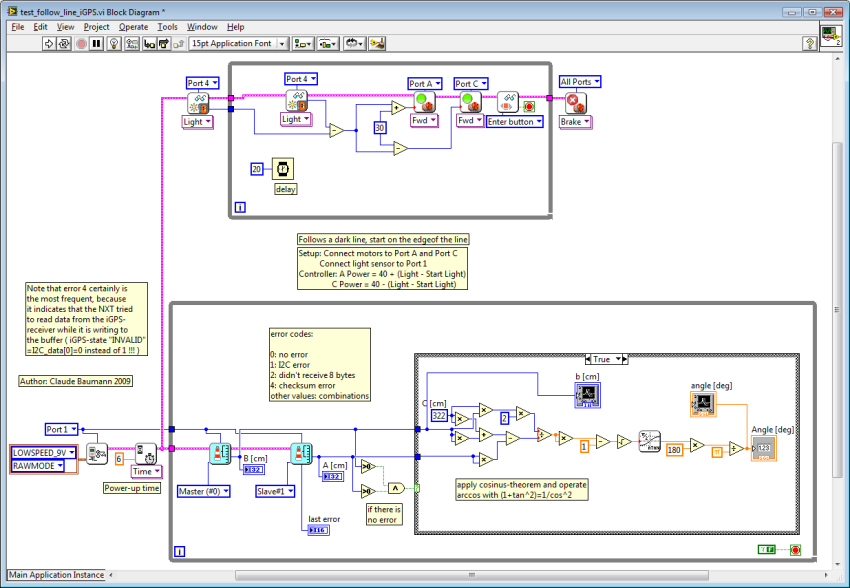
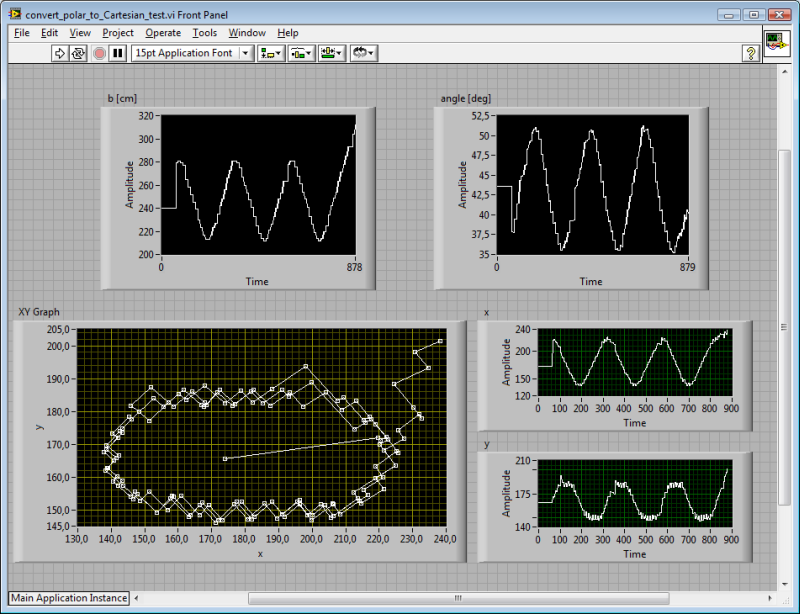
11. Follow a black line and localize the robot with the iGPS  

In order to test the reliability of the 2D-localization with the iGPS, we programmed the robot to follow a black line and upload the localization data to the PC. The program was run in debugging mode with the USB-connection. Then we "manually" dragged and dropped the data into a new VI, converted the polar coordinates to Cartesian coordinates and plotted the computed positions.

Notes:

  • Inadvertently we exchanged the master and the slave beacon, so the resulting graph is mirrored

  • The program uses the LVEE line-follow behaviour

  • The constant c=322cm was not measured, but just estimated. Its inaccuracy and the fact that we still ignore the height of the beacon locations explain the distortion of the curve.

  • The robot uses the light sensor in order to detect the black line. The algorithm does not produce the usual bang-bang line following, but a very smooth reaction.

  • The last turn, the robot lost the line and went off the oval.

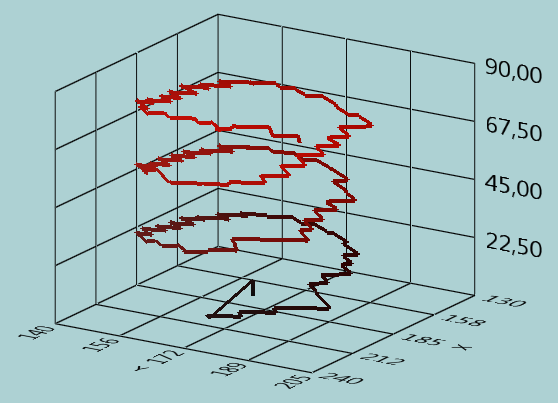
  • We draw a 3D-graph in order to show how the three turns that the robot takes overlay.

  • The zig-zag in the line come from the fact that the actual position is only deduced from iGPS data that is off phase by 250ms.

2009/10/27

12. Follow a black line, localize the robot with the iGPS, while processing the data with a 1st order Kalman filter

By now we have presented the scalar Kalman filter on this site. But, in order to efficiently navigate a robot with our iGPS system, we must this time implement a first order Kalman filter. This implies that we need to build a matrix-based filter that is able to describe the process as a state-space model with a state variable that is composed of a process variable and its derivate.

There are not many people who have played with the Kalman filter on LEGO bricks. Here a list of the most important available online work:

As usual we wanted to write the Kalman filter code in LabVIEW Educational Edition. There is one important limit to the implementation: the LabVIEW toolkit does not support 2D arrays. The solution to this issue is to reshape the 2D matrices into 1D-vectors and pick all the data from there. That's exactly, what we did. There are some important limitations:

  • The Kalman filter step function is limited to first order state space models and thus uses 2x2 matrices.
  • Since the LV NXT-compiler does not support 2D arrays, all 2x2 matrices are reshaped to 1x4 vectors, where the order is: a11, a12, a21, a22 (The first index indicates the row, the second one indicates the column)
  • The state variable is a 1x2 vector, because a first order state space model has only depth 2. (However, due to a compiler bug, the vector must be filled with zeros to 1x4.)
  • The measurement vector is 1x1 or 1x2. (Fill up with zeros to 1x4) The control vector is 1x1 or 1x2. (Also fill up with zeros to 1x4)
  • R must be 2x2.

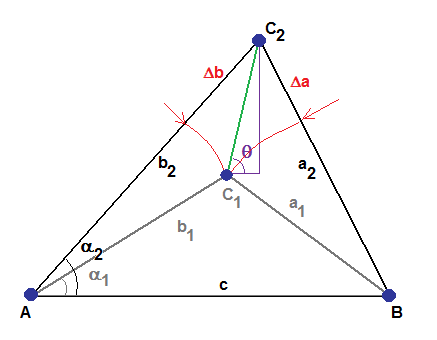
Now let's try to model the robot. First, we consider the black line as the planned path. We don't need to tell the robot more about the path, as we did in the 1D-experiment. Instead the line following algorithm and the black line are responsible for this task. To keep all linearity, we localize the robot in triangular coordinates, as explained above. Once localized, with no effort we can turn these coordinates either in polar or Cartesian coordinates. Because the triangular coordinates represent distances to beacons, let's denote the main variable r that represents the radius of the circle with center beacon  M  . (Practically, in our case, r either equals a or b and  M  is beacon A or B.) We have the equation:

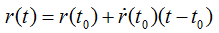
which expresses the fact that the next position is defined from the old one and its derivate (the speed). As a discrete time system, we assume that 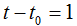and we prefer the index k to the time index t:

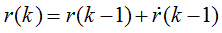
We define the state as:

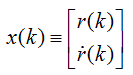
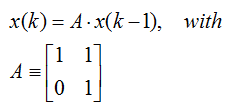
Recall the rules of matrix calculation. (A review is really indicated, before continuing)

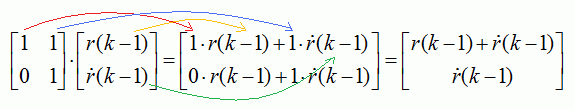
This equation suggests that the derivate does not change over time, which in reality is not true. Yet for the moment we will ignore that the process suffers from disturbances and is not submitted to control.

For now we only rely on one single measurement  z(k)  hat is related to the state variable through the equation:

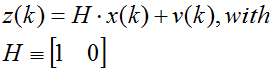
and where  v(k)  is the measurement noise. Note that the product of a horizontal vector with a vertical vector is a scalar and the noise  v(k)  has the same dimension.

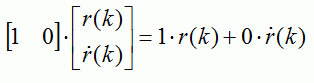
Thus,  z(k)  is a scalar (with matrix dimension 0). Notice that, when defining the parameters for a Kalman filter, it is always essential to follow the dimensions of the various matrices. The following schematics of the Kalman filter procedure has been copied so often on the web -without reference- that we reproduce it here with all the credits to the authors ( http://www.cs.unc.edu/~welch/media/pdf/kalman_intro.pdf ). Note that it was picked from THE  Kalman filter reference site: http://www.cs.unc.edu/~welch/kalman/index.html :

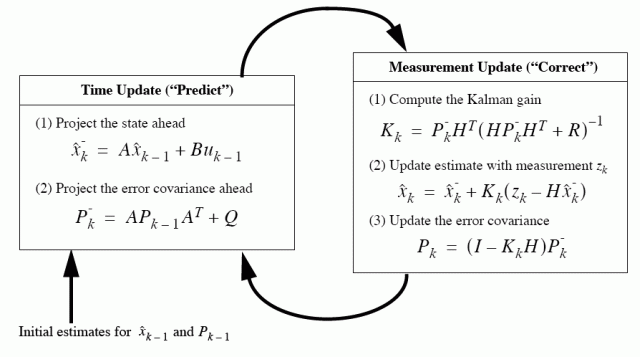
Q describes the process covariance. In the present example, the robot movement is part of the process noise, because in the equation above, we didn't add any control variable. In fact, B and u(k) are always zero in our example. Q and P have the dimension 2x2. We assume that the noise of the position and the speed are not correlated (which is obviously wrong, because any disturbance in the speed also changes the position and vice-versa.). Therefore the non-diagonal matrix elements are set to zero. Why such an assumption then? Q is one of the most important parameters of the Kalman filter. As Q gets smaller compared to the measurement variance R, the Kalman filter believes more the model than the measurement. Anyway, during the process, the error covariance, which is a fusion of the process covariance and the measurement variance, will show that the errors in position and in speed are correlated.

The dimension of the Kalman factor K must be 1x2, because in the Update equation (2) it multiplies with the scalar  z(k) . Remember that a few lines ago we underlined that  z(k)  had dimension 0. We also have seen that the product H.x(k) is a scalar.

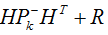also represents a scalar that you may easily verify through the following example:

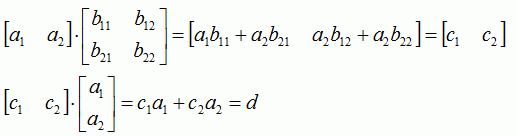
Hence, R must be a scalar. However, the current LabVIEW sub.vi does not verify the dimensions of the matrices. On the contrary, it is programmed to always operate the 2x2 inverse matrix. Therefore it is essential to design R as a 2x2 diagonal matrix with a dummy 1 in the right corner. Otherwise, the inverse matrix function will return an error value.

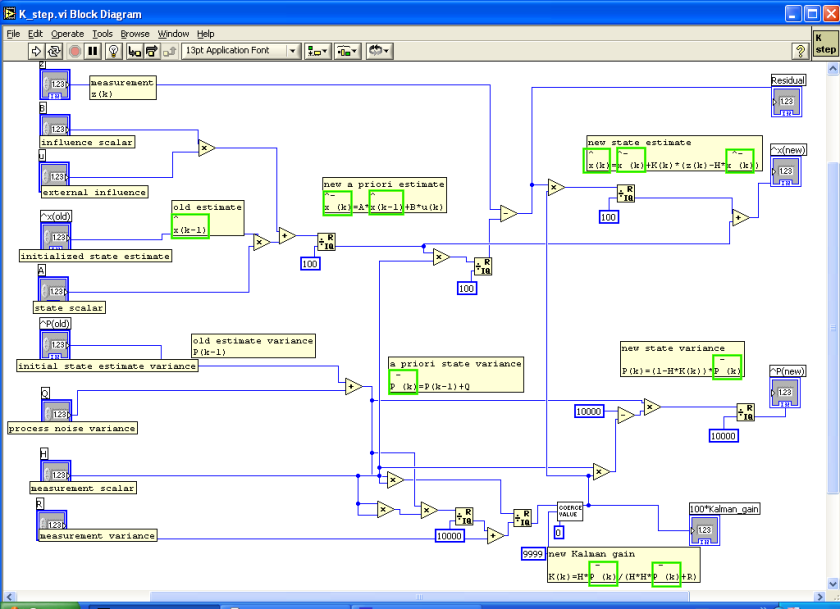
Here the first order Kalman filter step function. It looks impressively complex, but its execution only takes 15ms on the LEGO NXT, which must be considered as excellent timing.

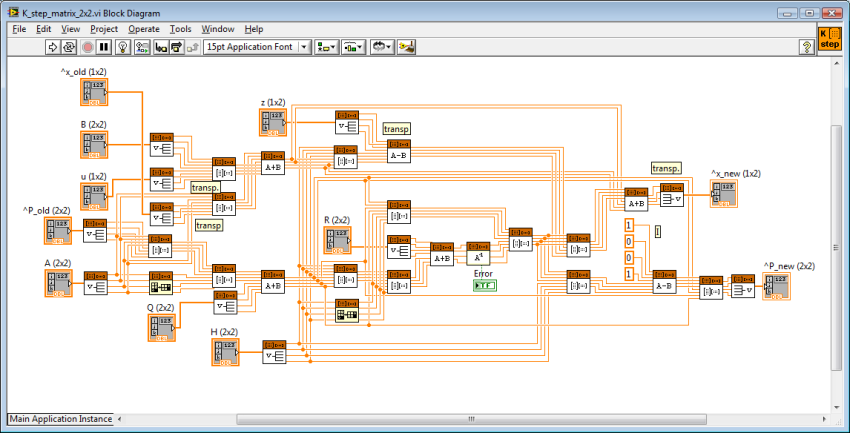
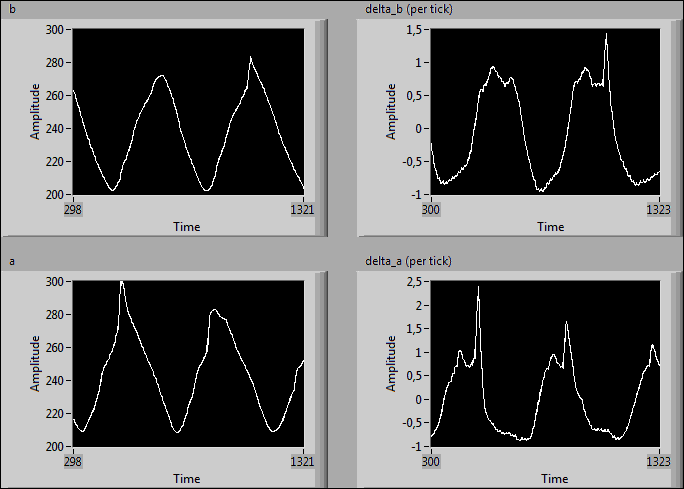
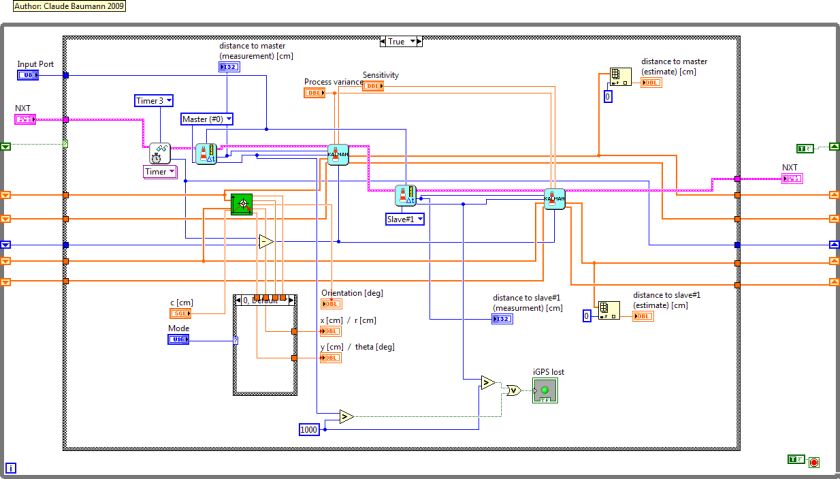
And the iGPS navigation program changes to the following diagram. Notice that we increase the variance R, if the iGPS data is invalid. The high variance tells the filter to ignore the last measurement. The reaction of the filter is very impressive. We could improve it, if we dynamically increased the sensor variance, as the duration from the last valid measurement increases.

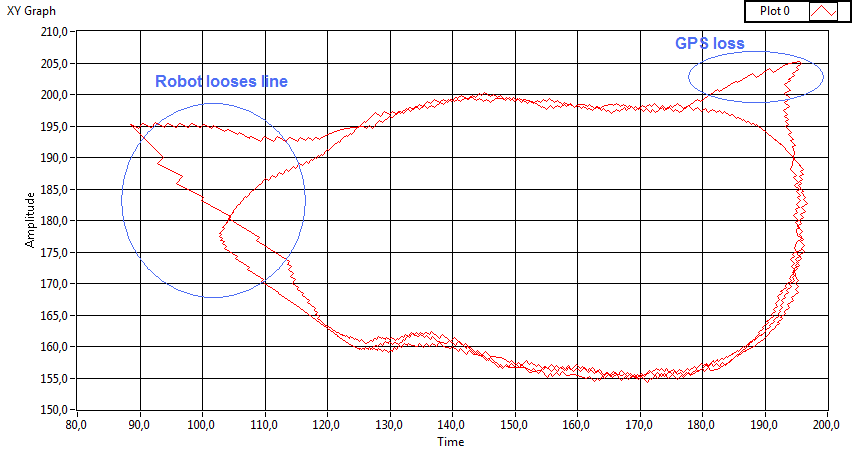
It is astonishing that the two events, on one hand the robot loosing the line, on the other loosing the iGPS signal, do generate the same kind of error in localization. The difference in reality was that during absence of the iGPS signal, the robot continued moving correctly on the line, whereas the second time, the robot completely went off the line and had to be replaced manually. Without any other knowledge, from the data alone, we cannot distinguish both cases. But, the loss of the iGPS signal can be compensated, if we add a second sensor to the system. We try to improve the data by dynamically adapting the measurement variance in function of the elapsed time since the last correct reading of a beacon value.

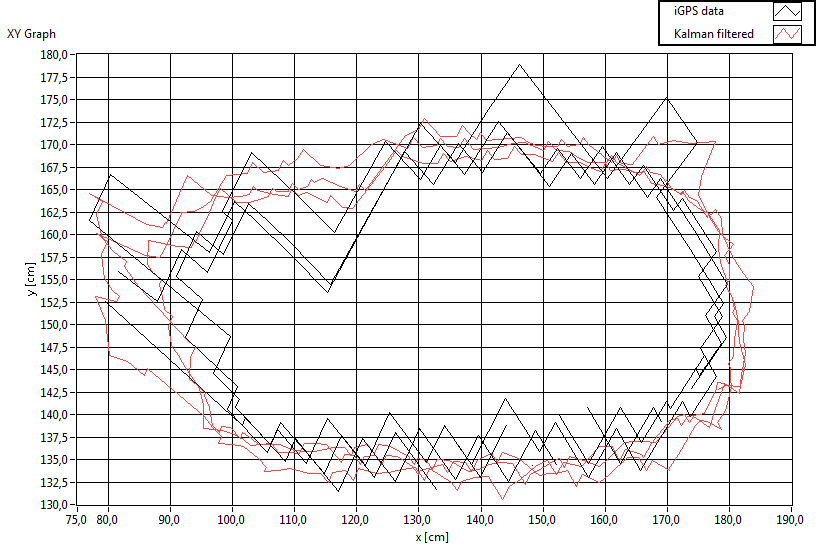
The following xy-plot is the result of a very small process variance Q=0.0001. Remember that this value, compared to R=1 indicates that the Kalman filter should believe more -but not explusively- the model prediction than the sensor reading.
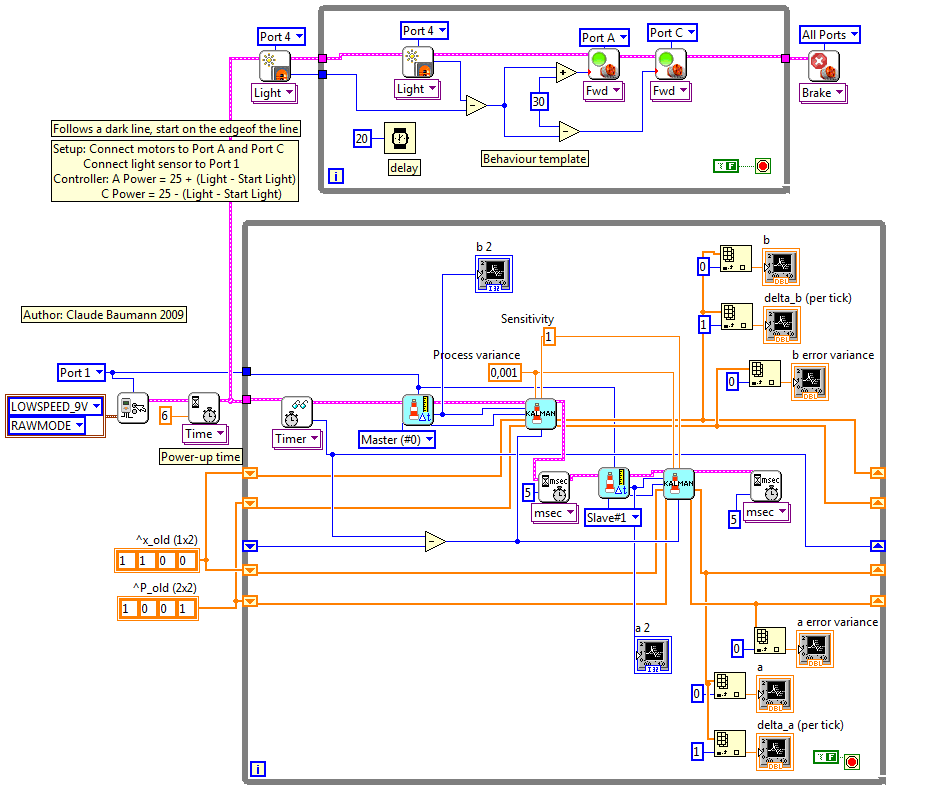
2009/10/28

We now use another iGPS sub.vi that returns the distance to the beacon and, for each beacon, the elapsed time in milliseconds since the last valid data. Obviously, if we have a valid measurement at a certain moment, we will have to wait 500ms, until the beacon sends again. During that time, the robot will displace by about 3cm and the sensor value that enters the Kalman filter has worse variance. Therefore, the iGPS Kalman filter function computes the travelled distance since the last beacon update and increases the measurement variance R accordingly. Now, the filter error variance is no longer fixed to the convergence value, but changes over time.

In the next example, the resulting graph is less smooth, because we tolerated a higher process variance. Note the additional variable "Sensitivity", that is a scale factor for the influence of the elapsed time since the last valid data.

  

 

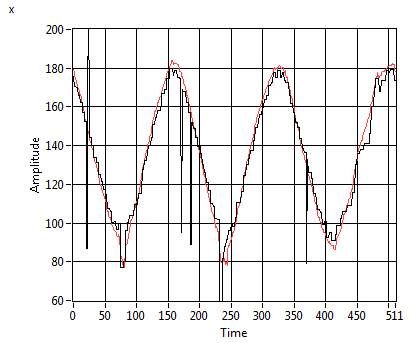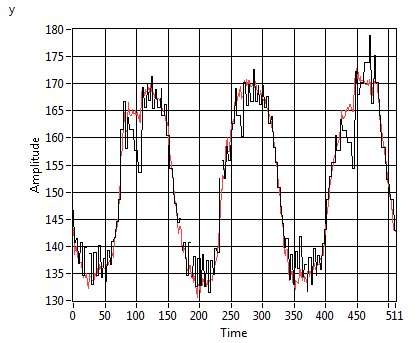
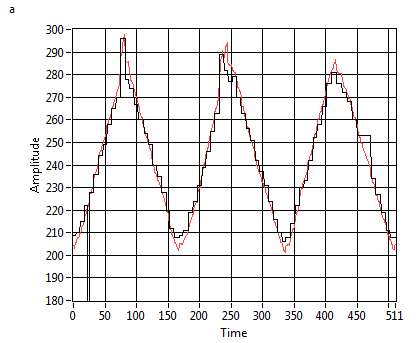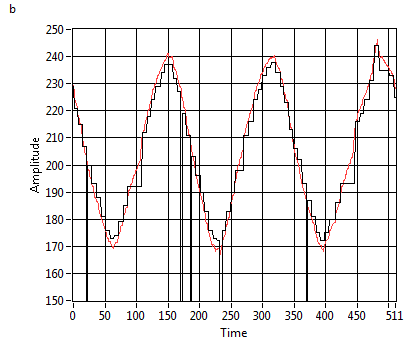
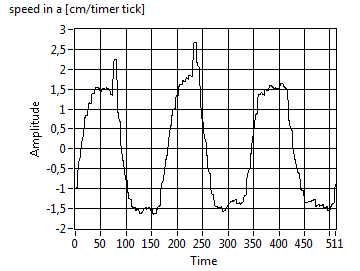
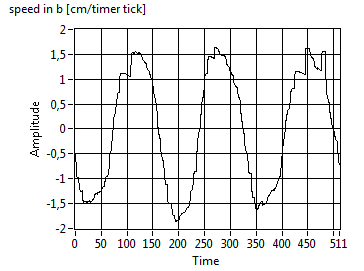
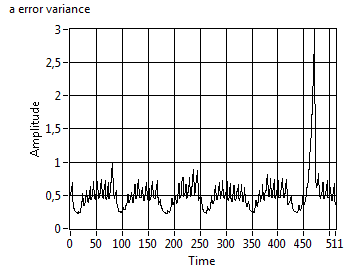
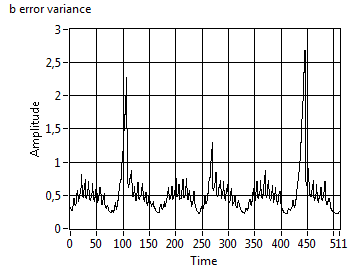
Tuning the filter is not too complicated. As a rule of thumb, we should compare (overlay) the measurement and the estimation, and adjust Process Variance and Sensitivity in order to get a smooth curve. We added a scale factor "h" to the iGPS_Kalman filter VI that helps squeezing the resulting curves. (Note that, if the filter is too strong, it looses actuality (phase-shifting) and also stretches the curves. So, for post data processing, a stronger filter might be preferred, but in a life application, actuality is more important.)

2008/10/29

The information that the iGPS system has gathered with the Kalman filter is sufficient to also yield the orientation of the robot. The main idea is to use the latest estimation of the beacon distances and the displacements in the triangular coordinate system and convert them to cartesian coordinates, while deducing the orientation. Anyway, since there is no other measurement of the orientation that might correct the prediction, we can assume that this estimation will be the best that we can do. Thus, this ahead fixing of the robot orientation will depend on the overall error of the filtered data. However, because the transformation into Cartesian coordinates is no longer linear, the error will not propagate in a linear way either. The easiest way to estimate the errors that propagate through the non-linear system is applying the Gaussian method. Here a few references that introduce this method:

If the variance of the orientation is needed, the program should include the calculation of two discrete derivates and apply the error propagation formula for variances.

Another idea is to operate a Taylor linearization of the non-linear functions and tranform the Kalman filter into an Extended Kalman Filter (EKF). (This is not indicated here, since the actual matrix Kalman filter is only implemented for 2x2 matrices.)

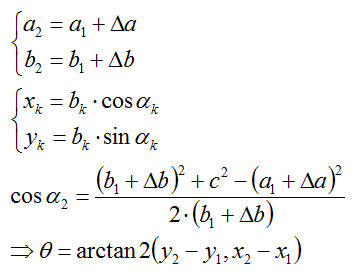
Another test gives us the orientation during a robot run over the circuit:
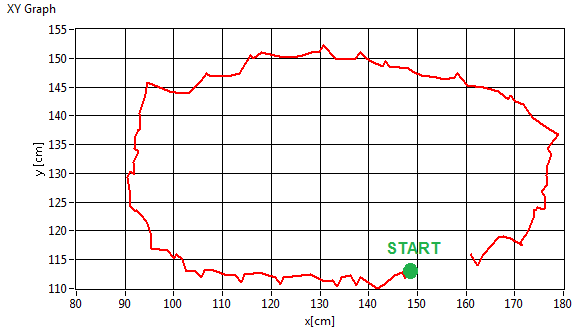
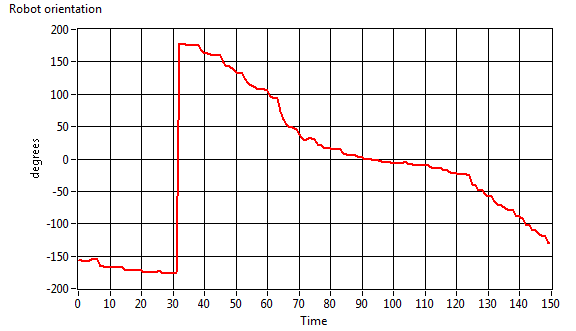
2009/10/30

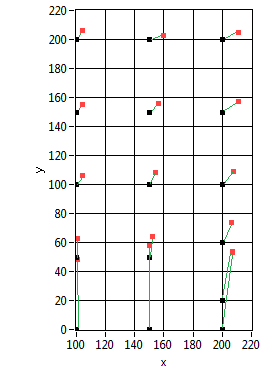
13. Convert the triangular coordinates into Cartesian coordinates

Now the program should convert the triangular coordinates from the iGPS trilateration into Cartesian or polar coordinates. As we already pointed out, this conversion-functions are no longer linear. For our present project however, this does not matter, because with the excellent precision of the iGPS distance data, error variances can be assumed very small. But, we will test this. The LabVIEW program that is run in debugging mode appears very smart:

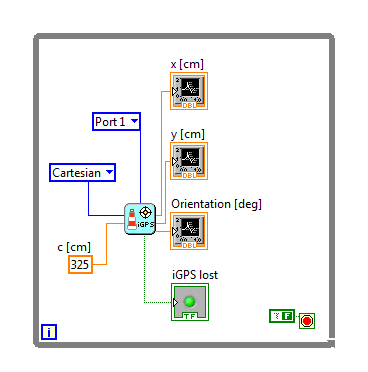
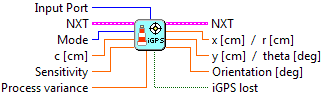
For it was possible to run the device with approximate beacon positions. Also we corrected the offset by a constant (25cm that we tried to explain above - probably we were wrong in the interpretion).

  • We noticed that weak beacon 9V block-batteries have an effect on the offset, although the receiver is stable for beacon battery voltages down to 8,3V. Below this value, the offset grows.
  • There are no differences between the master and the slave beacon. (A study here can only be made, once we have more beacons.)
  • The NXT voltage does not affect the readings.
  • We took off the plastic reflector, because we found that the shadow on the IR-receiver was too bad and also increased the offset.
  • The offset is slightly dependent on the distance. So, we add a correction function to the main distance extractor VI. (d=1.0191*x+4.2133).

The very first tests yields the following graph

  • Note that the results are based on the Kalman filter data and that the filter has not been fine tuned yet. from the graphs above, you can see that the filter slightly overestimates the true values
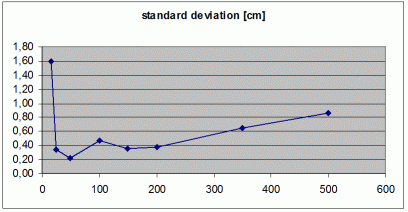
  • The standard deviation never exceeds 1 [cm] both in x and y.
  • The graph is very similar to the thoroughful study of the Höhrmann's project, from which we pick the error-graph of a simulation with a two-beacon scenario. 
  • Beacon spacing was 325cm
  • Errors are largest between the beacons

Conclusions: The results can be improved, if the Kalman filter is tuned. This however may take quite a long time.
2009/10/30

14. Some more tests

  • long range test without reflector:
    • beacon and receiver aligned: maximal measurable distance 16.40m
    • beacon at 2m height, receiver horizontal: maximal distance 5.70m ==> might be an idea to rethink about using a reflector; but the plastic reflector above hides the IR-receiver!!!
  • The team will build 2 more beacons. So, there will be 4 and complete 3D-positioning will be possible.