- Main references :
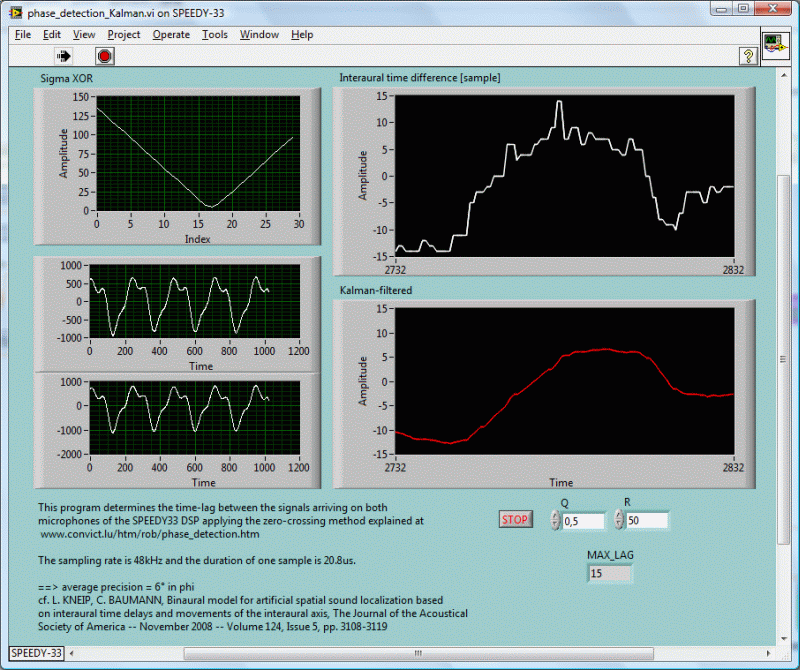
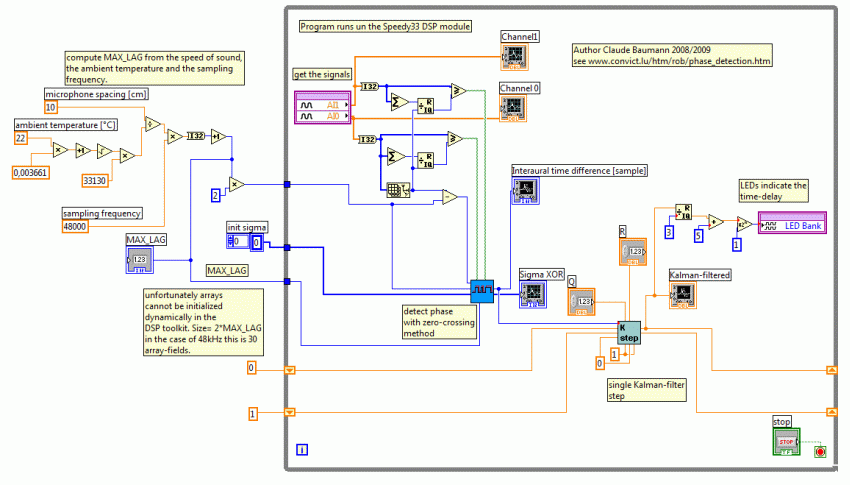
- Phase detection NXT robot (explains the algorithm)
- Spatial sound localization (uses the cross-correlation method)
- Introduction to the scalar Kalman filter (external reference)
- Material: NI DSP toolkit (see photo)
- Download: DSP project for the binaural phase detector

In the presence of very weak signals -probably below the noise threshold- the program tends to move back to the middle position, although there are significant fluctuations. We already met this issue in our Elektor project (Article: C. BAUMANN, L. KNEIP, Stereo robot ears, Elektor, July/August 2007, p. 13-17 , where we added a sensitivity potentiometer to the circuit that tells the microcontroller software to ignore the audio noise beneath the threshold. There also is the option "relative", that can be set through a jumper telling the microcontroller. If it is set, the device considers the position to the sound source as "relative", and the result of the measurement is zero. This could be interesting for a robot that is moving the head in the direction of sound, where the position of the sound source is referred relatively to the orientation of the head. However, imagine that a video-camera system would try to move the fixed camera to a sound source, then an "absolute" position should be observed, and in the case of weak signals the system should hold the last valid position in order to avoid swinging of the camera. In a next version we will add this feature to the DSP-program.
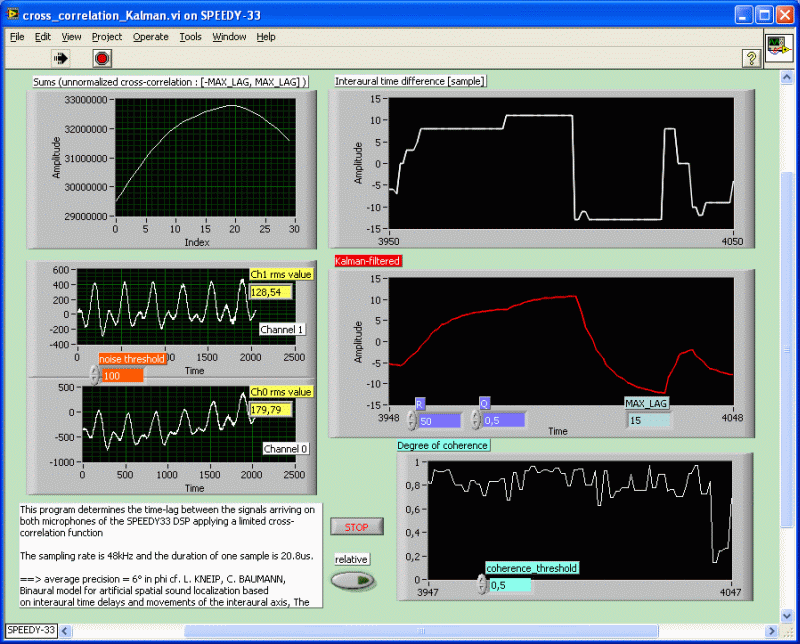
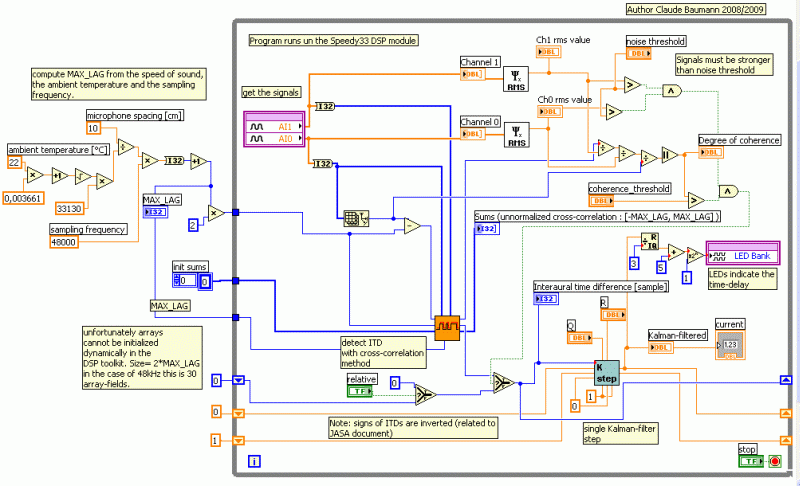
Consult the following figures, if you want to understand how the program works. You should be familiar with LabVIEW. During the program execution the DSP was still connected to the PC, in order to have the live data upload and to produce the data graphs. The scalar Kalman filter follows the equations and notations that are developed at http://www.swarthmore.edu/NatSci/echeeve1/Ref/Kalman/ScalarKalman.html .
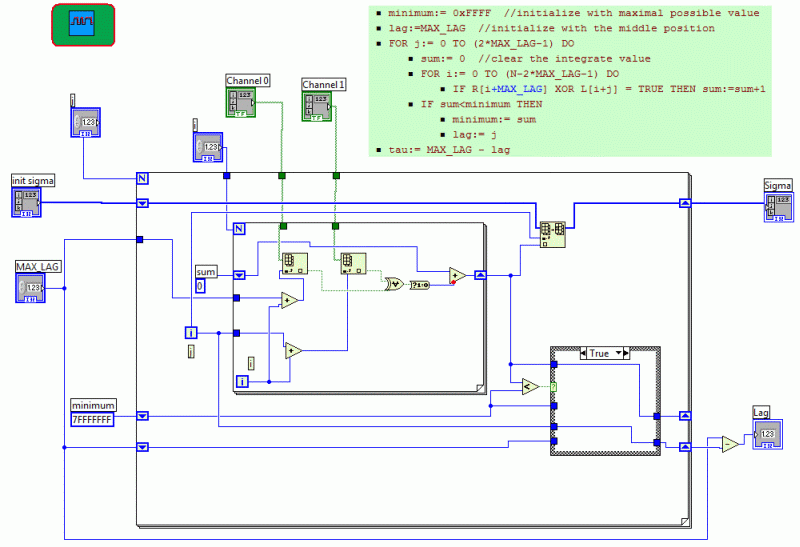
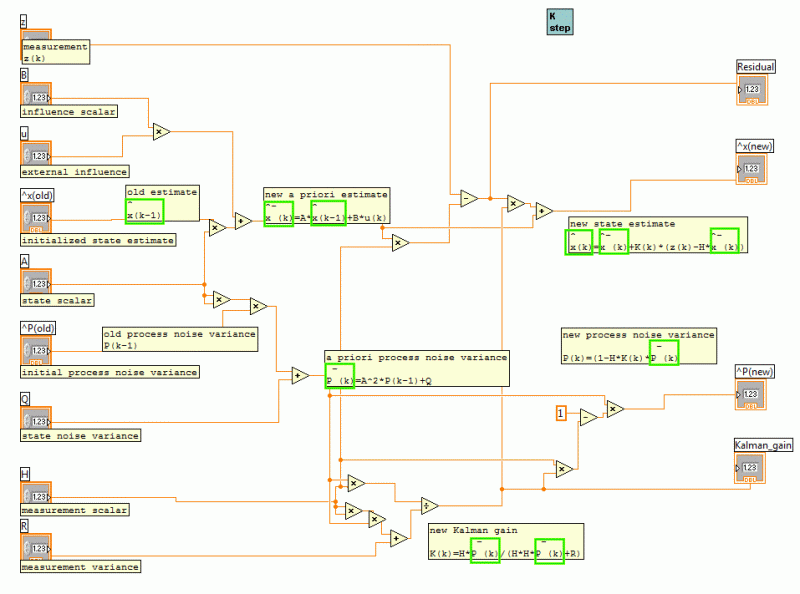
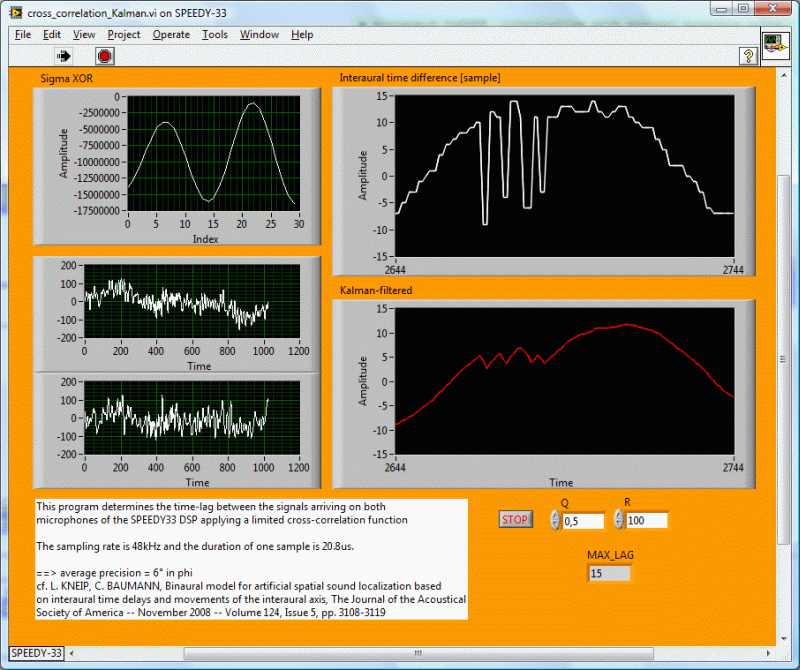
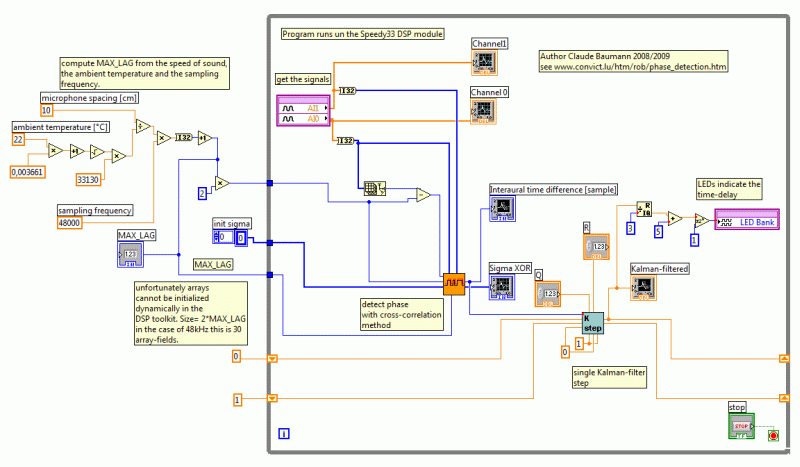
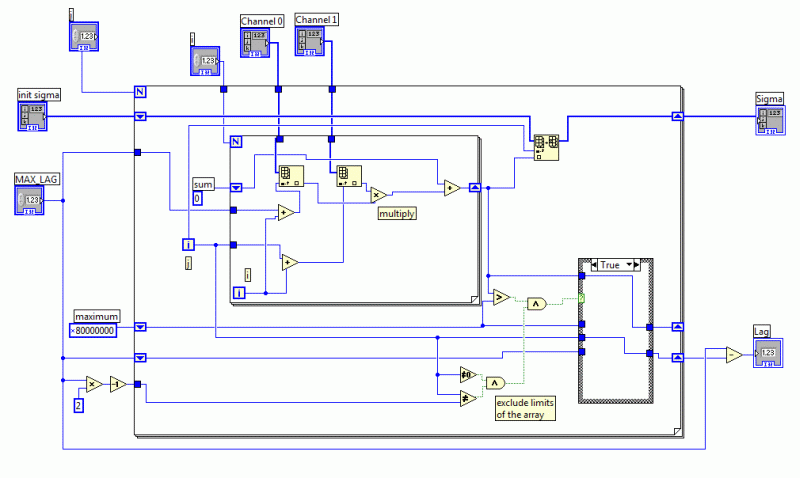
The combination of the scalar Kalman filter with the degree of coherence and noise suppression stabilizes the output. We fixed the DSP module on a rotating base. A phone-cell (Sony Ericsson G700) was placed at 1m from the Speedy-33 at azimuth beta_0=125° and elevation omega=-13°. The cell was playing mp3 encoded music. The cross-correlation program yielded a time-lag of 7 units (correct -7, since signs are inverted in the program, because of the graphs). Then the Speedy-33 support was turned by -30° around the z-axis. The new azimuth beta_1=155° was calculated from the new time-lag -12.4 using the Kneip/Baumann algorithm that is explained at (Spatial sound localization). Note that one unit has the duration of 1/48000sec, because the sampling frequency is 48kHz. The estimated location is beta_1*=149° and omega*=15°, within the theoretical error limits that are fixed according to the mentioned algorithm.