NAVIGATOR

The autonomous navigator

Last update:

13/3/2001: Erased another bug in the break task (delta_y is not xy_diff !!!) Download the new version in the download area below.
10/2/2001: Erased a bad overflow-bug in the program. Now possible to enter magnitudes up to 110 dm. The magnitudes have to be entered in dm-unit, no more in cm!! The Sinus look-up table has been replaced by a polynomial approximation -->gain of speed (look-up table needed +/- 0.19 sec to find a sinus, new approx needs only 0.08 sec.)

The new program is called AURORE2

The SINUS approximation is the formula for angles from 0..45 degrees:

100*sin(x) = -0.352173719 + 1.845955302*x - 0.005761952*x*x

This formula has to be adjusted to the integer problem:

100*sin(x) = { [ { [ (x*71 + 5 ) div 10 ] * 26 - [ ( x*x div 5 )*57 ] div 20 -35 } div 10 ] + 5 } div 10

between 46..90 degrees: the result is given by: sqrt(10000-100*sin(90-x))

Here the LeRobot subroutine:

beginofsub(sinus)
   if(var,angle,GT,con,45)
     setvar(flag,con,2)
     mulvar(angle,con,-1)
     sumvar(angle,con,90)
   else()
     setvar(flag,con,1)
   endif()
   setvar(result,var,angle)
   mulvar(result,con,71)
   sumvar(result,con,5)
   divvar(result,con,10)
   mulvar(result,con,26)
   subvar(result,con,-35)

   setvar(h1,var,angle)
   mulvar(h1,var,angle)
   divvar(h1,con,5)
   mulvar(h1,con,57)
   divvar(h1,con,20)

   subvar(result,var,h1)
   divvar(result,con,10)
   sumvar(result,con,5)
   divvar(result,con,10)

   if(var,flag,eq, con,2)    {case angle greater than 45 deg}
   mulvar(result,var,result)
   setvar(arg,con,10000)
   subvar(arg,var,result)
   setvar(result,con,100) {first approx}
   loop(con,4)           {Heron's alg. for square-root}
      setvar(h1,var,arg)
      divvar(h1,var,result)
      sumvar(h1,var,result)
      divvar(h1,con,2)
      setvar(result,var,h1)
   endloop()
endif()

endofsub()

This is our second attempt to realize an RCX-robot able to navigate freely to a given point T(a,d), where a represents the phase of the vector OT and d its magnitude. The phase is exprimated as a clockwise compass-angle.

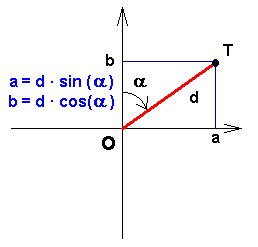
The robot should read the compass-direction using the PEWATRON compass-sensor, then read the travelled distance during a certain time, compute the actual position, adjust the course and finally, decide the motor-control accordingly. All this is done similary to the algorithm explained at the honey-bee and robot navigation page.

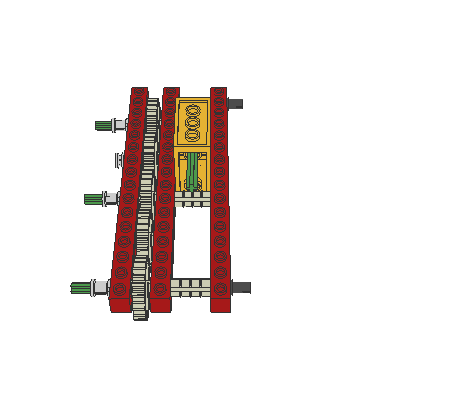
The following robot design (an altered Mars-Rover) shows an important detail: the differential gearing is used as an adder. So, if the robot is turning, the rotation-sensor will not register any change. This simplifies the program-design, because the robot may continuously check the actual position without error. Otherwise the rotation-sensor will notify advancing, whereas the robot only executes zero-turning.

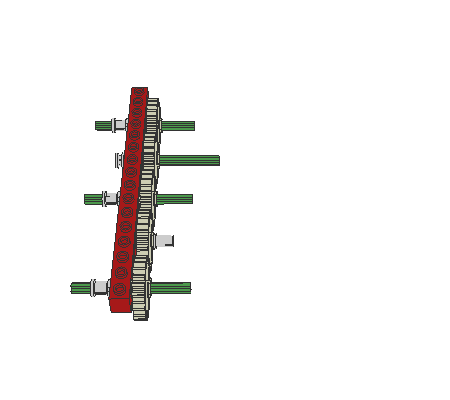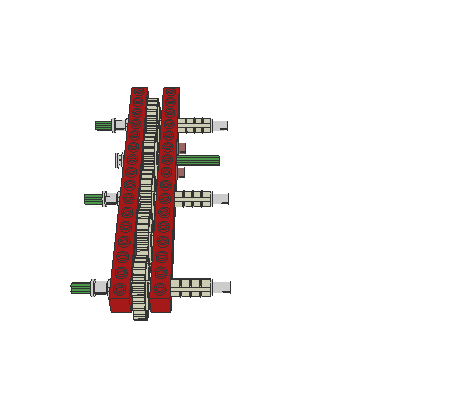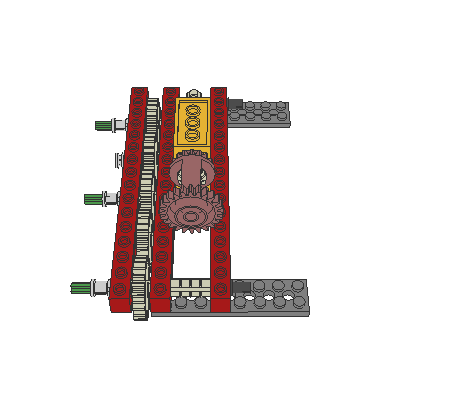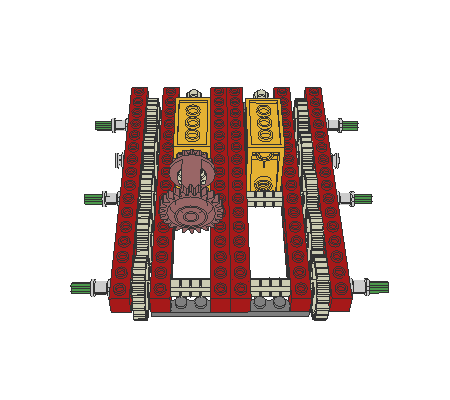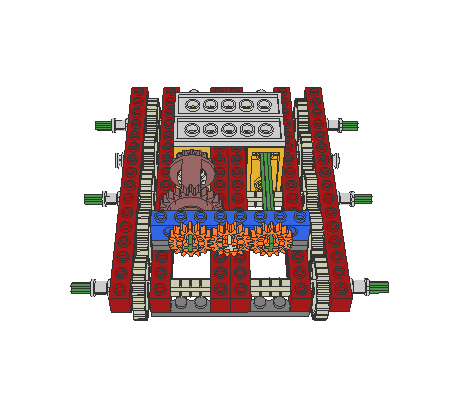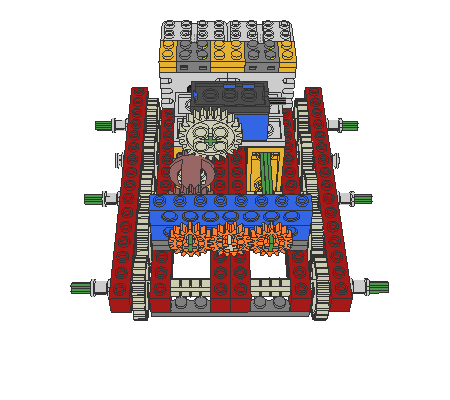Finish the robot by adding the RCX, a double bumper and the compass-sensor. Connect the compass-sensor to port 1 and 3 AND connect the left bumper to port 1, the right bumper to port 3. (Yes, this is possible!!!) Connect the rotation-sensor to port 2, the left motor to output A, the right motor to output C.

Download the LEOCAD and the LeRobot files. You'll need the new LeRobot version!!

Do not forget first to run the CALIBRATION program, then the NAVIGATOR.

The target point T may be entered by sending directly to the RCX: the phase a to variable 28 and the magnitude d to variable 29.

As you may see, the robot tries to surround obstacles and nevertheless arrives at the given target.

ATTENTION: this robot is rather slow but it has a big resolution. The precision is remarkable ~ 4 cm.

Main page