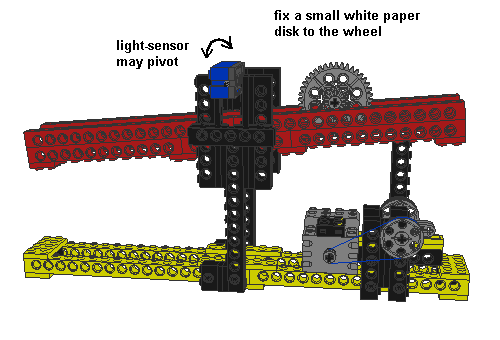
An improved version of Philippe Hurbain's seesaw


We try to balance a free turning wheel on a seesaw. Quite simple for humans, but for a robot, it's a real challenge. This tiny robot-challenge brings us to very exciting physics:

Planopedia: http://philohome.free.fr/seesaw/seesaw.htm . Download our slightly transformed version as a Leocad-file: seesaw.lcd

Two major factors act on the system: the moment of decision to flip coming from the sensor's redings and the flipping speed which can be influenced by the transmission ratio. In order to reduce parasite movement and provide perfect symmetry, specially identical slope-angle on each side, pay attention to the correct position of the 6 holes-wheel (6-way symmetry vs 4-way of the axis).

We added 2 transformations from the original design:

  1. For precise sensor-reading: fix a small white paper disk to the sensor-sided part of the free wheel.
  2. In order to set the flip-instant precisely, the sensor has been fixed that it can pivot. So we can determine its best position.

The seesaw should be well balanced.

 R = D/2 = 20,75 mm (40 teeth-gear assembled as shown)

r = d/2 = 3,75 mm

m : mass of the wheel

g = 9,81 gravitation constant

acceleration of the translation movement:

a = m / (m + J / r2) * g * sin(alpha)

J : inertial moment of a cylinder = m/2 * R2

by simplifying we get for the used Lego piece approximatively:

a= +/- 8/13 * sin(alpha) {up or down}

sin(alpha)=1 cm / 12,75 cm

{ length of a 1 x 16 Lego-brick : 12,75 cm; the seesaw slopes 1cm }

so: a= +/- 0,0483 m/sec2

(During the flipping time, a must be expressed as: a= - 0,0483 * cos(theta), where theta is the instant angle of the wheel linked to the motor by the rubber. This produces a curved reverse of the acceleration, but for these calculations can be ignored.)

Friction of the system causes the amplitude to diminish at every turn. This has to be compensated by lengthening the descending slope by L. We have:
  • x = a * t2 / 2 : formula for constant accelerated movement which is equivalent to: x = a * T(x)2 / 8 for a whole periode of two movements.
  • ==> T(x) = 2 * SQRT(2 * x / a)
  • so: Tmax(xmax) = 2 * SQRT(2 * 0,1275 / 0,0483) = 4,6 sec
  • standard movement: Tst(xst) = 2 * SQRT(2 * 0,1 / 0,0483) = 4 sec
  • T(x') = SQRT(2 *(x + L) / a) = SQRT(2 * (xst - L) / a)
  • ==> x + L = xst - L
  • ==> L = (xst - x) / 2
  • ==> T(x') = SQRT(x + xst) / a)
  • ==> T(x') = SQRT( ( T(x)2 + Tst(xst)2) / 8)
  • dt = T(x') - T(x)/2

We wrote a somehow tricky program. The difficulty is to force the RCX to calculate a square-root with only integer variables. The whole movement is divided into 3 phases, each beginning with a pass of the wheel in front of the light-sensor:

  1. clear the timer
  2. register the actual period length T(x), start the calculations (which need some time) to determine dt
  3. before flipping, wait the time dt to compensate the difference between T(x) and Tst(xst).

A three times version works as well, but in this case the period is measured alternating the side.

{ SEE-SAW robot}
{...tasks...}
#define(calculate,1)
{....subroutines...}
#define(SQRT,0)
{...variables...}
#define(threshold,0)
#define(ActPeriod_length,1)
#define(WaitTime,2)
#define(counter,3)
#define(value,4)
#define(argument,5)
#define(res,6)
#define(h1,7)
#define(result,8)
{...constants...}
#define(MotorOnTime,50)
#define(precision,6)
#define(little_bit,2)
#define(StdPeriod_length,40)
#define(SQRStdPer,1600)

selectprgm(slot_2)

beginoftask(main)

setsensortype(sensor_1,light_type) {set sensor parameters}
setsensormode(sensor_1,percent_mode,0)

setvar(threshold,con,0) {threshold is average of 40 values}
loop(con,40)
setvar(value,senval,sensor_1)
sumvar(threshold,var,value)
endloop()
divvar(threshold,con,40)
sumvar(threshold,con,precision)

setpower(motor_a,con,7) {first go to initial position}
On(motor_a)
wait(con,MotorOnTime)
Off(motor_a)

loop(con,forever) {check the light_sensor and decide}

setvar(counter,con,0) {reset the counter}

Loop(con,3) {3 phases}

sumvar(counter,con,1) {add to counter}
while(senval,sensor_1,LT,var,threshold) {wait until wheel passes}
endwhile()
{---}
if(var,counter,eq,con,1) {clear timer}
playsystemsound(click_sound)
cleartimer(timer_1)
setvar(WaitTime,con,0) {clear WaitTime}
endif()
{---}
if(var,counter,eq,con,2) {measure timer}
setvar(ActPeriod_length,timer,timer_1)
starttask(calculate)
endif()
{---}
if(var,counter,eq,con,3) {define WaitTime}
setvar(WaitTime,var,result)
endif()
{---}
wait(var,WaitTime) {wait during dt}
AlterDir(motor_a)
on(motor_a)
wait(con,MotorOnTime)
off(motor_a)


while(senval,sensor_1,GT,var,threshold) {wait until object far away}
endwhile()

endloop()
endloop()
endoftask()

{==========================================}

beginoftask(calculate)
if(var,ActPeriod_length,LT,con,StdPeriod_length)
setvar(result,var,ActPeriod_length) {example: 20}
mulvar(result,con,10) {needed later for calculation with hundredth of seconds}
divvar(result,con,-2) {200/(-2)=-100}
setvar(argument,var,ActPeriod_length) { 20}
mulvar(argument,var,ActPeriod_length) {400}
sumvar(argument,con,SQRStdPer) {1600+400=2000}
divvar(argument,con,8) {2000/8=250}
mulvar(argument,con,64) {250*64=16000, trick to stay below the integer limit}
gosub(SQRT) {sqrt(16000)=126}

mulvar(res,con,10) {real res is actual res*10/8==>res=158 which is sqrt(25000)}
divvar(res,con,8)
sumvar(result,var,res) {-100+158=58 1/100 sec}

else()
setvar(result,con,0) {clear the result, zero waitTime}
endif()
stoptask(calculate)
endoftask()
{==========================================}

beginofsub(SQRT)
setvar(res,var,argument) {initial value}
loop(con,10) {do the Heron's iteration 10 times}
setvar(h1,var,argument)
Divvar(h1,var,res)
sumvar(h1,var,res)
divvar(h1,con,2)
setvar(res,var,h1)
endloop()
endofsub()

A NQC-version will follow soon.

This is a nice example of a robot that may not be realized by what Seymour Papert calls "bricolage", but by deduction.

 

Main Page