Robo-Soccer Journal

last update : 25/02/02

29/01/02

This will now be our major project for the second semester of 2001/2002.

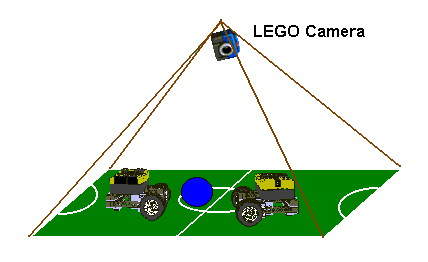
The aim is to make two semi-autonomous LEGO-Mindstorms robots play soccer in a given field of 1.20 m x 1.60 m.

Most of the mobile robotics professionals and amateurs know about the difficulties which appear in this project. You'll have to deal with game strategies, speed, collision-avoidance a.s.o. 

Primitive robots might possibly play the game, but there is too much random, which will surely make them loose. This is of course not compatible with one of the aims of playing soccer that is to win ! You'd have a great advantage if the soccer player knew :

• where he is
• where the ball is
• where the goals are
• where the opponent player is

So again we have to deal with the positioning problem.

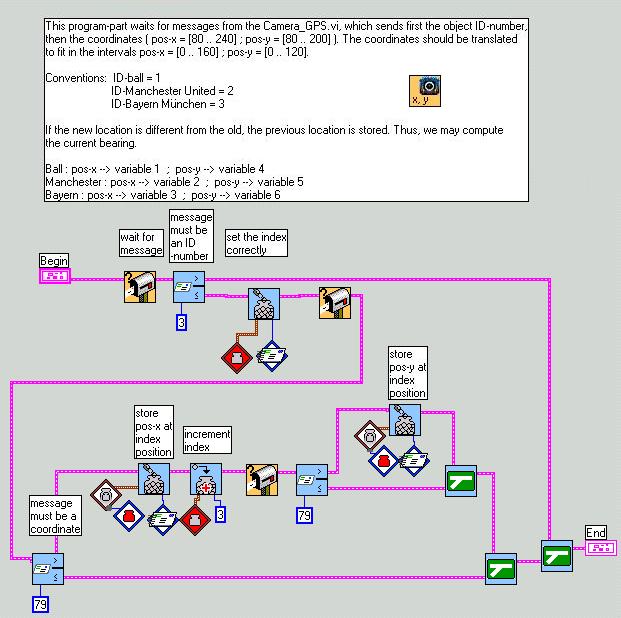
Our solution will be a global positioning system based on the LEGO camera which is fixed at the top of 4 wooden sticks. Thus it will survey the whole game and find the positions of both mobile robots and the ball. A special program will continuously analyze the pictures, then send the coordinates and perhaps other data like current direction and velocity to the two RCXs via IR-communication.

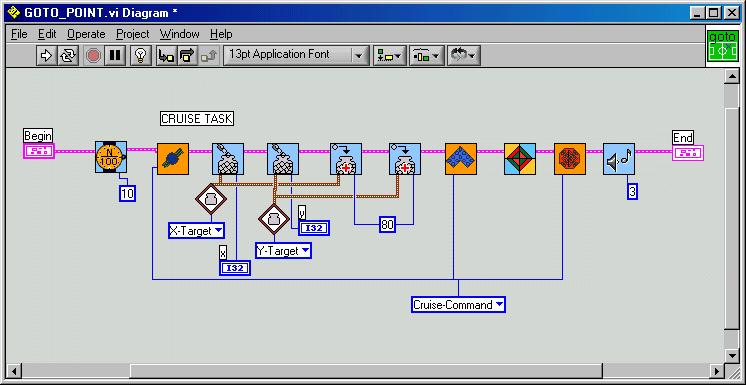
Based on this information each mobile robot should then be able to play soccer according to the strategy of choice.

Preliminary problems to solve:

• design a robust camera support
• based on the Robolab 2.5 multimedia feature create a software that will be able to fix the positions of the given objects and broadcast-send the information to the involved RCXs.

30/01/02

• the LEGO camera may be used for global positioning.

01/02/02

• The positioning and the communication works GPS.

04/02/02   In the field

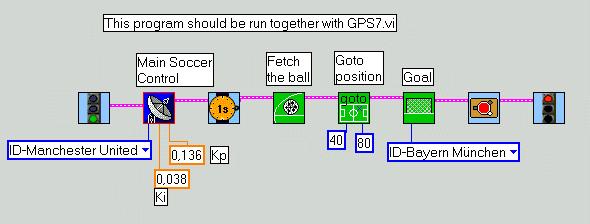
The first tests with a real robot-soccer-player was done with the test-program Soccer2.vi.

You'll recognize the subsumption architecture and lots of new sub.vis which all may downloaded here as Robolab-libraries :

Robo-soccer, Subsumption architecture, Camera_GPS. (versions 4/2/02)

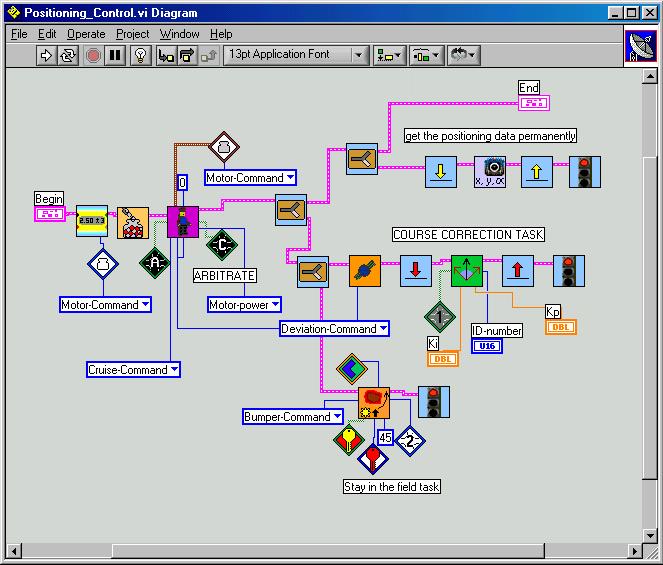
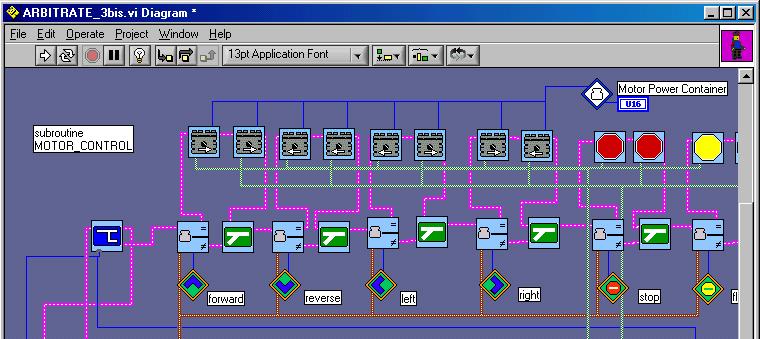
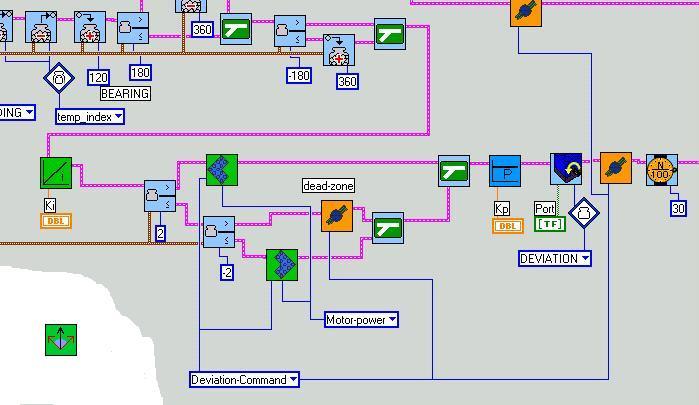
Here some pictures of the most important vis.

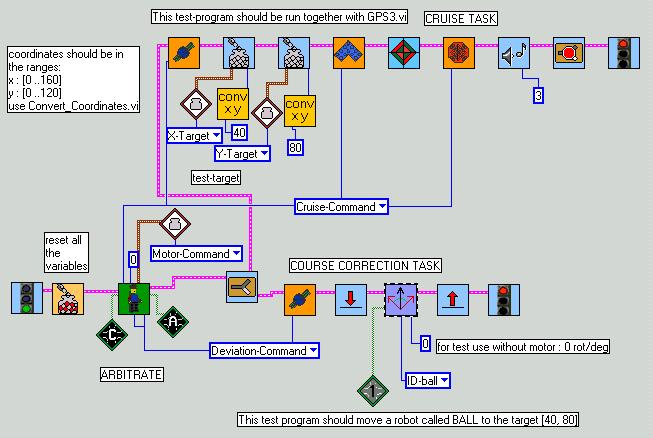
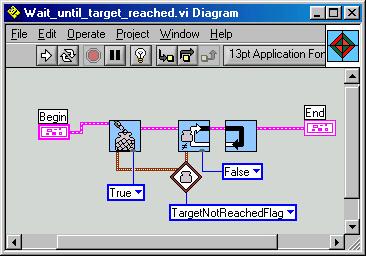
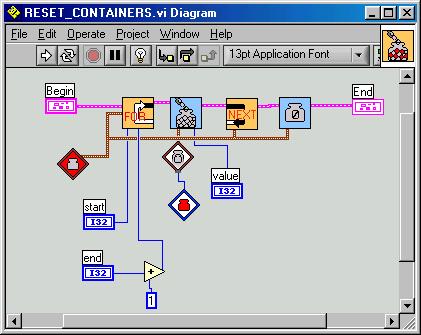
Yes, we've designed a simple FOR-NEXT-loop.

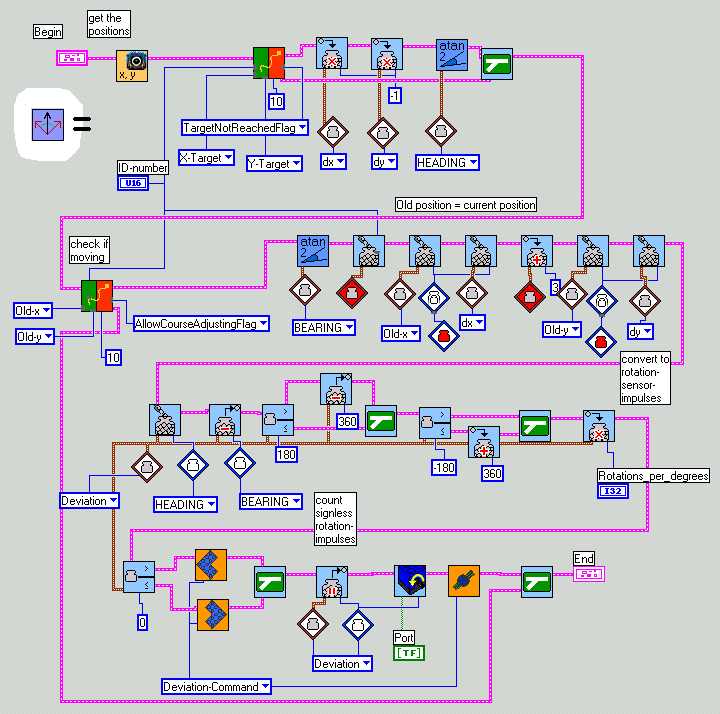
During the first tests all went well. The coordinates arrive from the GPS3.vi. As you can see, the course is only adjusted, when there has been an update with new coordinates AND when these are different from the previous ones. Only with this information the robot is able to find its bearing, for it actually needs two distinct points to do so. Without correct bearing, the course may not be corrected properly.

VARIABLE LIST

05/02/02

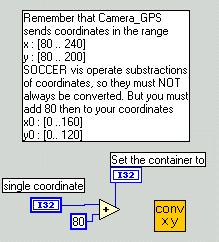
The general idea was to fix the robot's (or the ball's) position through the center of mass-coordinates which are computed in the Camera_GPS programs. This is done very well ! The communication to the mobile robots works well too. But: real world is not ideal world !

As we could probably have expected: serious problems occured in the BEARING-fixing task.

The planned strategy was on the robot-side to update the current position only if it had changed more than a certain tolerance.

From the division :

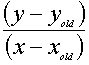
we can easily extract the current bearing. The new heading is computed and it is checked, if the robot has already reached the target.

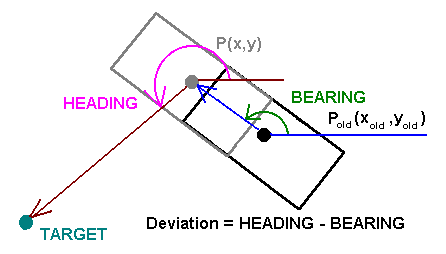
The robot fulfills then a rotation around its central axes (which should be the center of mass of the camera-observed robot-shape) to compensate the course deviation. So, in theory, during the turning the center of mass does not move.

In reality however, the camera-GPS-system registers a motion of the central point during rotation, for several reasons:

• the zero-turning point is not the same than the center of mass of the projection-picture in the camera

• the camera-plane is not absolutely parallel to the playing-field. So, the projected shape changes during rotation

• the very first bearing is wrong, since oldx and oldy are zero at start !

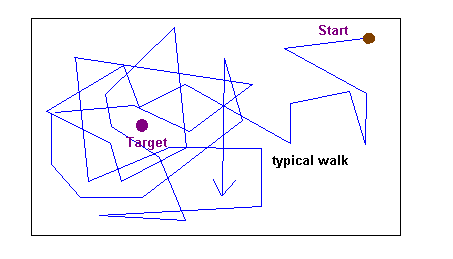
So, what did we observe? The robot was travelling around and operated unexpected rotations. But, it constantly moved around the target, never reaching it.

7/2/2002

We detected another problem of the programs GPS3.vi and Soccer2.vi :

• There is an important relationship between the image-refresh-rate (which is in fact the positioning sampling-rate), the object-velocity and the threshold we set in order to decide whether yes or no the coordinates have to be updated in the RCX. This has no major influence on the reading of the object-location (a certain tolerance is acceptable), but leads to a chaotic interpretation of the current bearing.

By the way, a further Camera_GPS version could include the possibility to flip and mirror the final blop-image. This would make human interpretation easier, since the orientation of the on-screen cartesian system differs from that in reality.

During the team-discussion about this problem there were several proposals:

• Scharel : mark the center of rotation by a lamp. So the camera-software could easily locate the exact position.
• Juri : if lamps are used, the ball must be illuminated too or analyzed in a different filter
• Max : use two smaller color-blops for one robot instead of one big blop. This corresponds to the ideas expressed in the document Integrating Active Tangible Devices with a Synthetic Environment for Collaborative Engineering (National Institute of Standarts and Technology)

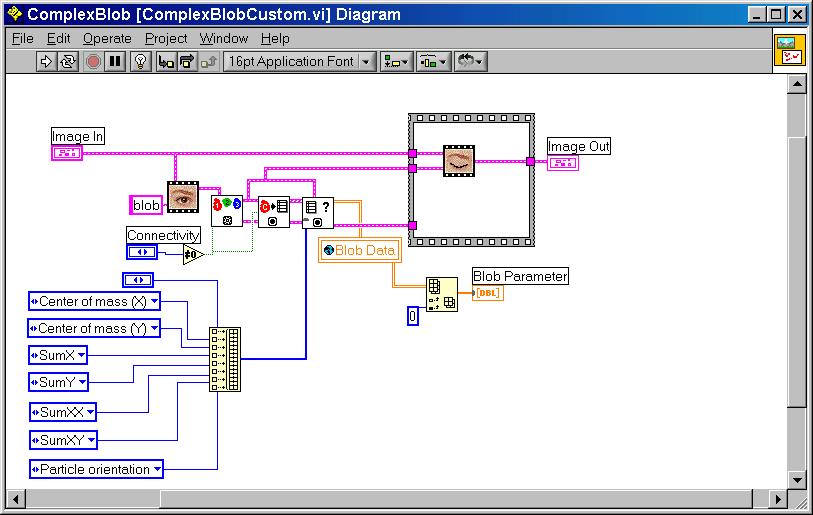
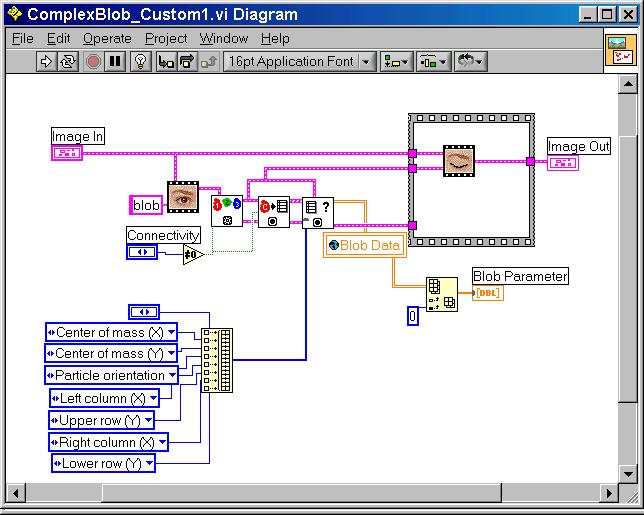
The IMAQ ComplexMeasure.vi (more than the IMAQ ComplexParticle.vi) from the Robolab ComplexBlop.vi permit to extract more information than only the blop-area. There is a longer list of data among which you find : particle orientation, number of holes, center of mass, Sx, Sy, Sx², Sxy ...

Here a picture of the customized ComplexBlop.vi which enables the extraction of the additional data:

18/2/2002

It appears that the particle orientation yields only angles between 0 and 180 degrees. To make a correct bearing-decision possible we add a particle-hole to the observed object. In this case the center of mass ( G ) and the center of the particle ( C ) - defined as the center of the global rectangle - are no longer identical. Thus we may decide whether the center of mass is situated above or below the particle-center.

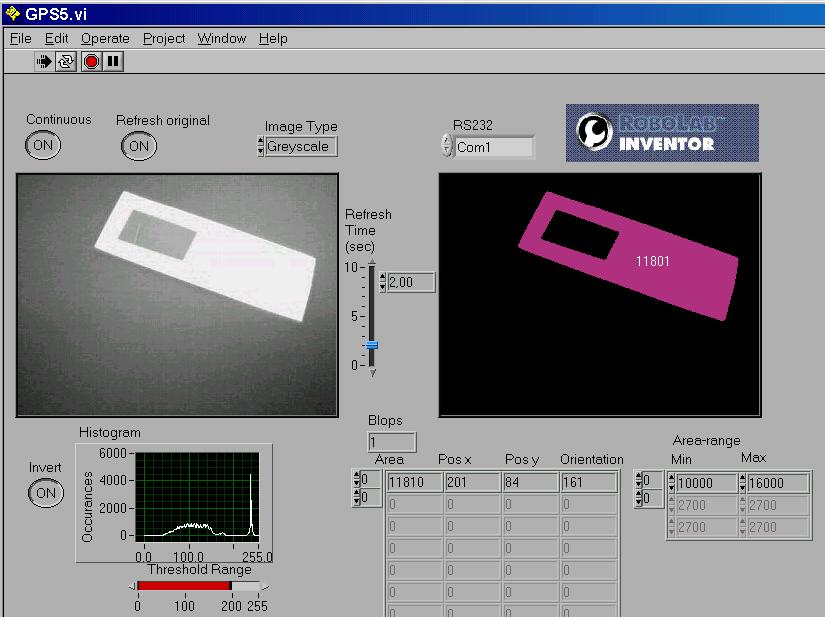
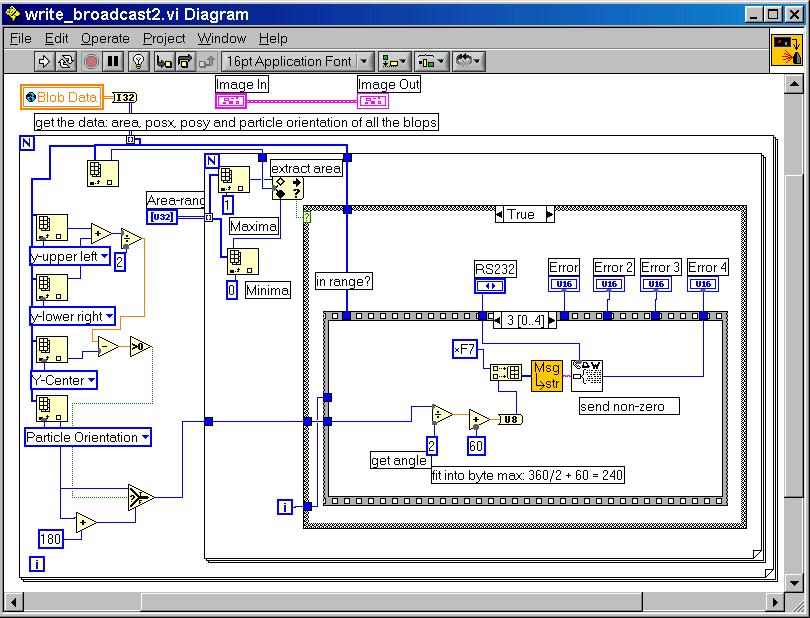
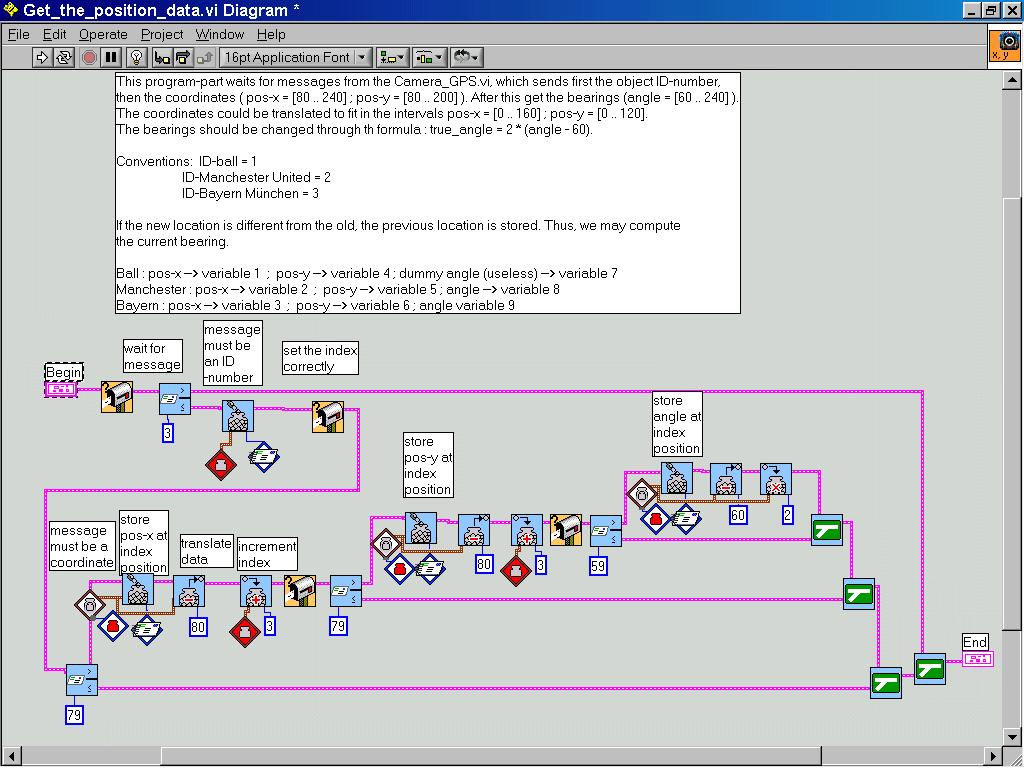
This leads to the altered GPS5.vi which uses the ComplexBlob_Custom1.vi and the write_broadcast2.vi .

It may be tested with the read_and_display_angle.vi equipped with the Get_the_position_data.vi.

19/2/2002

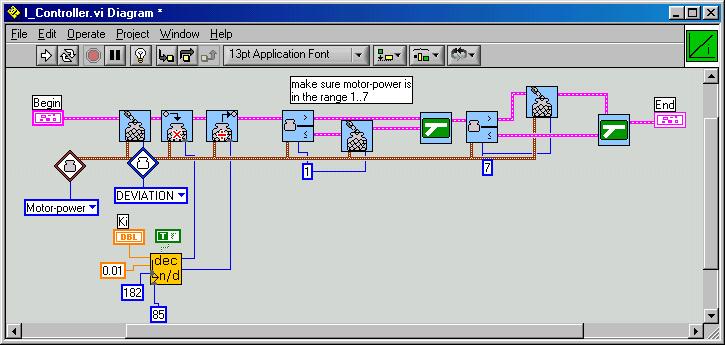
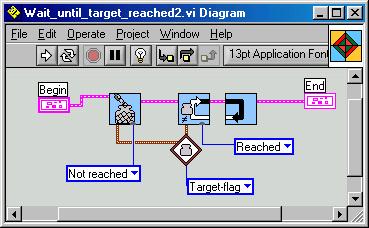
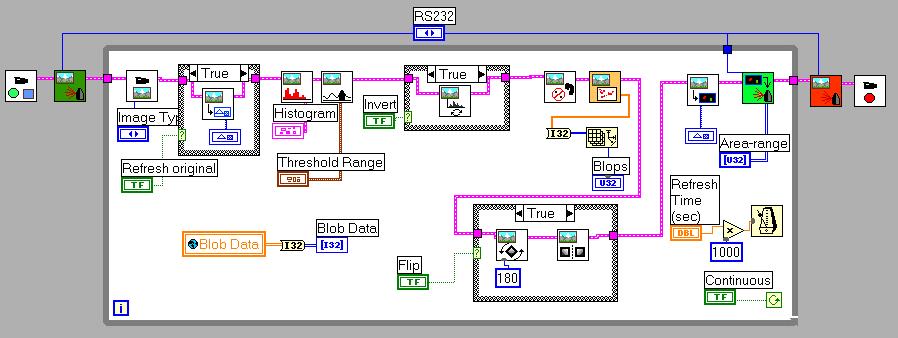
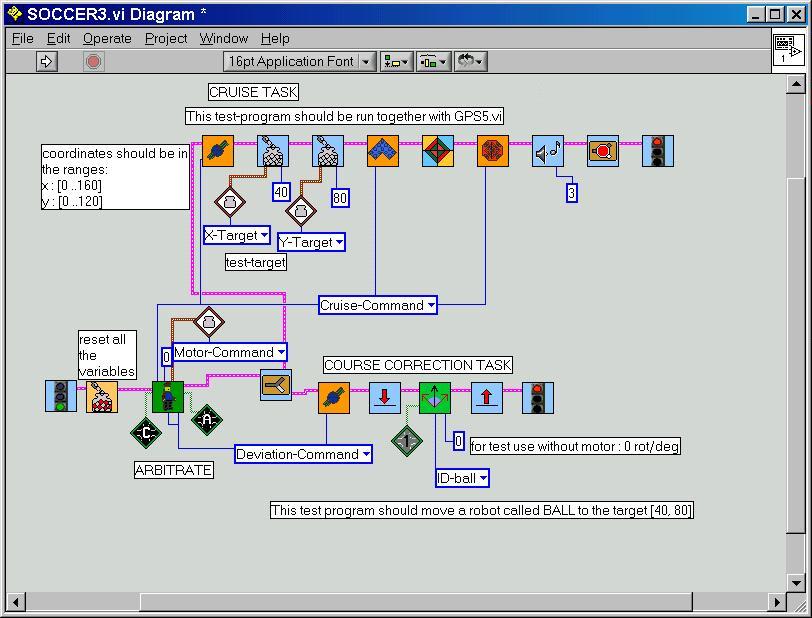
Here now the GPS6.vi which allows flipping of the blob-picture for better readability. Note that the Robolab-original Rotate.vi has a small bug that we have corrected : the designers have forgotten the connection to the flipping angle. The write_broadcast3.vi has a slight change in the angle computation due to the different cartesian orientations. Soccer3.vi allows a first alone robot to reach the target-point [40,80]. It uses the Wait_until_target_reached2.vi, the Correct_course2.vi, the Motion_and_target_test2.vi and the Get_the_position_data.vi from above.

Note that we have a different variable-list now and that the coordinates are immediately converted to fit in the range [0..160] resp. [0..120]. The angle is returned in a 2° resolution.

GPS6.vi :

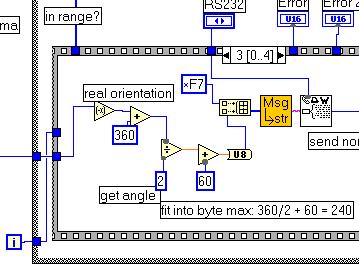the write_broadcast3.vi changes

23/02/02

The tests with the new programs have been successful. The mobile robot immediately took the direction to the target, but oscillated around the correct course. At every course adjusting the robot overshot a lot.

The causes:

• The sampling rate of the camera-GPS system is clearly too slow (max: 10Hz). This has major effects, when the robot executes short turns. Our robot needs 2.4 seconds to fulfill a complete turn of 360°. A 10° rotation needs only 66ms (!), which -according to Shannon - would need a minimum sampling rate of 2* 1/66 = 30Hz.
• The beep in the correct_course.vi is in a bad place ; the rotation-sensor is cleared and monitored only after a certain duration while the robot is turning without control.
• The multi-tasking, especially through the implanting of the subsumption architecture, there is a considerable delay between notifiying and execution of a motor-command.
• The robot advances during the course-computations, so the current heading is never correct. (This should not lead to overshooting, but rather to the contrary)

The solutions:

• The IR-communication should be done in an independent task. The positioning variables are considered as global, so no computations will be done directly on them.
• The course-correction task must then have a local index, not to disturb the storage in the communication task.
• The rotation-sensor values should be scaled down proportionally.
• The Camera-GPS program should include the possibility to switch off the drawing of pictures to speed up the transmission.

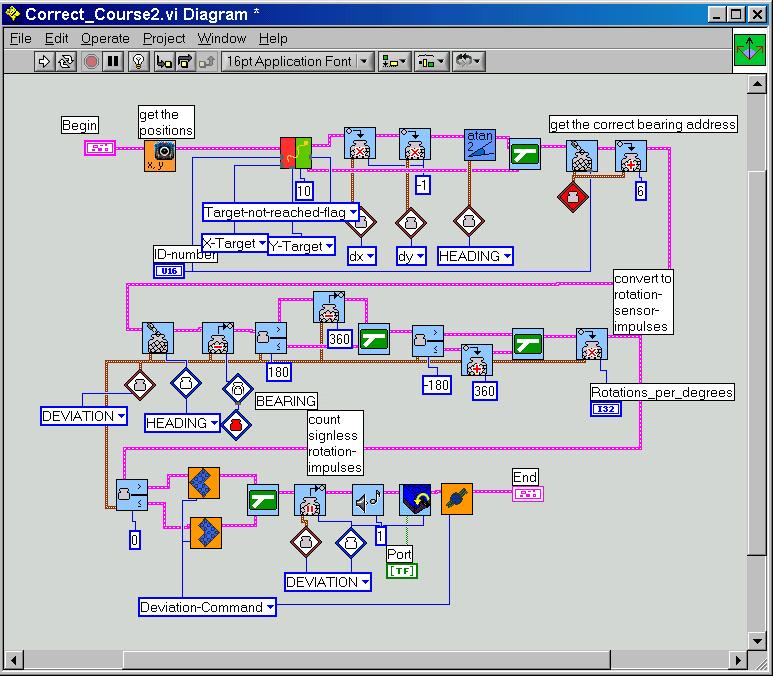
Here a major transformation to the Correct-course2.vi:

GPS7.vi with an additional switch looks like:

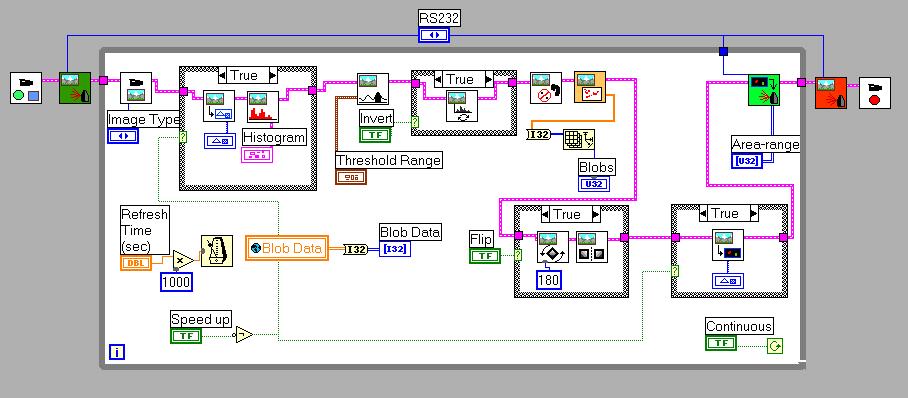
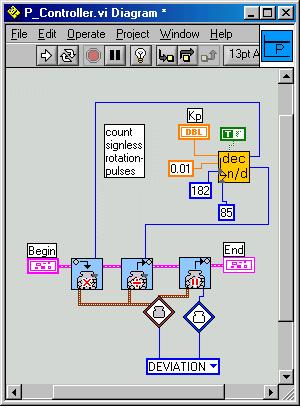
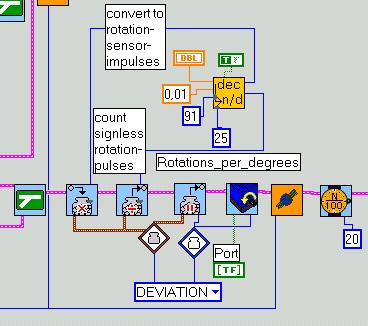
Where Conv_dec_to_quotient.vi is a special Labview-routine to convert decimal values to a division of integer numbers needed to scale the rotation-value.

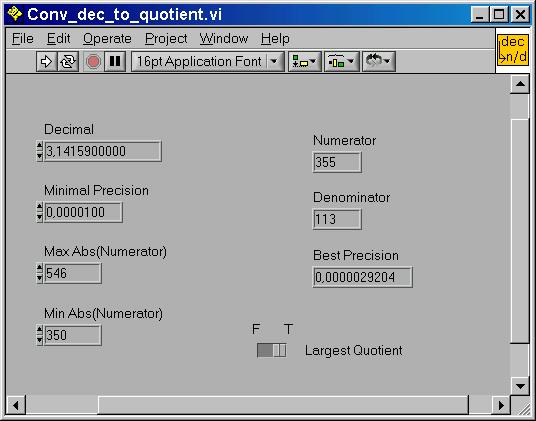
a ~= n / d,   a: decimal; numerator, denominator: integer

Example: 

You want to scale the contents of a variable x by factor a=3.14159. This is difficult with the RCX, which allows only integer operations. The trick is to find  the two numbers n, d, to multiply x by n and divide by d. You must observe not to trepass the 32767 (resp. -32768) integer-limits while multiplying.

The accuracy depends on the range of x and of course the values n and d. The higher the value n, the more accurate the scaling will be. By multiplying the decimal-part of x is converted to an integer part.

Let x be an integer of the range [-60,60]. The maximum absolute numerator is 32767 / 60 = 546. Our desired precision is 1E-5. We want the numerator as high as possible, so we set the lower limit to 350 and the switch to largest quotient. The program issues the values n=355 and d=113 as shown.

Test with x=57 :

y = a ^. x = 3.14159 ^. 57 = 179.07063

y' = n ^. x / d = 355 ^. 57 / 113 = 20235 / 113 = 179.0708

NOTE : this LABVIEW-routine acts on constants only. It will NOT be included in the RCX-program. But it makes constant scaling easy. The program notifies by an error-message if no quotient was found. If you include the program as sub.vi in an Robolab program this will not stop downloading. But you'll know that your constants are wrong.

25/02/02

The tests with this altered course correcting task shows that the oscillations can be reduced. Now the robot reaches its target much quicker than in the previous experiments. But some unexpected behaviour has still appeared.

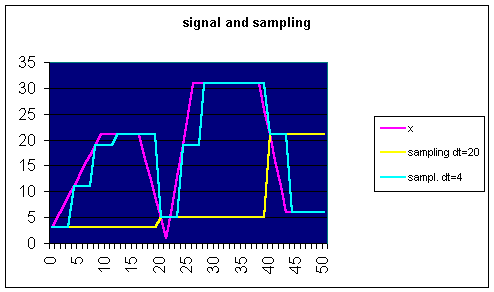
This picture illustrates well the sampling problem. Over a certain limit the sampled values do no longer correspond to the original signal. The information gets lost.

The sampling frequency should be at least twice the signal frequency.

In our case of a linear Lego-robot motion at a speed of about 0.4 m/sec, the camera-GPS sampling rate is largely sufficient. But as pointed out, if rotating this is not true.

Here a graphical analysis of the error-sources :

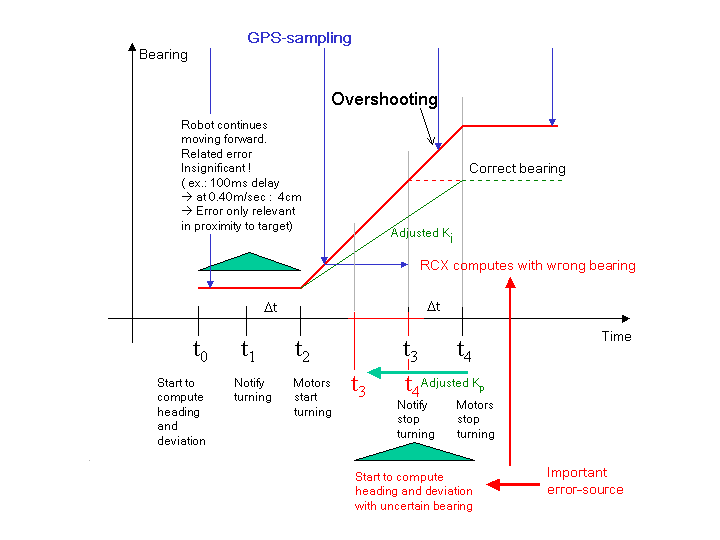
There are actually two major problems:

• The delay between computing, notification and real motor-action which is due to the use of the subsumption architecture, to multithreading and low computing speed of the RCX. In fact the process is a PT₁-system with an additional dead-time part T_t, which we we are trying to  through a P(proportional)-controller. The controller output is proportional to the process-error. Through optimizing of the proportional factor K_p, the oscillation of the process may be minimized.

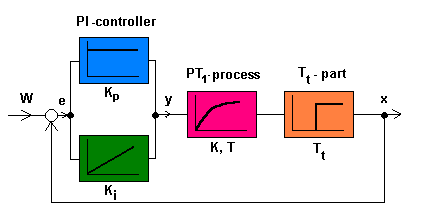
where W is the heading, x the bearing, e the course deviation, y the controller output (in rotation-pulses). Note that we omitted the load which acts on the final knot.

• After the stop turning notification the RCX may start computing with bad bearing values. This doesn't happen necessarily everytime, but explains the unexpected behaviour noted above. To overcome this problem, the RCX must at least wait until the next GPS-update (given by the Camera-GPS refresh-rate).

The process might be improved through an additional I(integrate)-controller, so that we are in front of a real PI-controller. In the case of an I-controller, the variations of the controller-output are proportional to the control-error. This is not the usual definition, since it is mostly difficult to influence the derivate of the controller-output directly, but the reasonment is equivalent to saying that the controller-output is proportional to the accumulated error. Considered in that way, the implementation is not complicated, since the motor-speed must only be proportional to the course-deviation. Thus, a large deviation will produce a rapid course-correction and a small deviation a slow correction. The non-standard use makes the tuning of the PI-controller a bit tricky. The best procedure is to follow parts of the Zeigler-Nichols technique and the try-and-error technique:

1. The I-controller should first be disabled by setting motor-power constantly to maximum. Tune K_p with low values up to the point where the robot starts oscillating. Note the value of K_{p_crit}  and measure the period of an oscillation : T_p. Now set K_p = 0.45 ^. K_{p_crit} . Note that in our case the value of K_p depends on the number of rotations per degree.
2. Enable the I-controller and find the best value of K_i by try and error.

There exists a huge number of interesting web-sites dealing with the PID technique. There is one particular site which explains the implementation under LEGO-Mindstorms : Using a PID-based Technique For Competitive Odometry and Dead-Reckoning. You'll get some basics at Tuning fundamentals and Back to Basics.

By the way, some other interesting sites around our project here: Camera Positioning, Soccer playing, a master thesis about robo-soccer, Picture handling, some Robolab-links, Robolab in school (German).

26/02/02  FOR SERVER-MEMORY REASONS, SOME PREPLIMINARY SUB.VI -LINKS ARE DEFINITELY BROKEN, YOU'LL FIND THE MAIN DEFINITE FILES SOON IN THE DOWNLOAD AREA.

Here now the implementation :

FINAL WORK AND DOWNLOAD AREA

Main Page