Square-root based on CORDIC

We explained the CORDIC basics for trig-functions earlier. The solution of exercise 2 of that page will be shown here. But some preliminary explanations.

Perhaps you know the following card-game:

You tell a candidate to select and remind a number from 1 to 31. Then you show him the following five cards one by one. He must answer the question whether the number is yes or no written on that card. By miracle you can tell him the number he chose. The card-order is irrelevant.

The trick is to mentally add the first number of each card where he answered YES.

Let's take an example: the candidate chooses 23

How does this game work?

By answering yes or no, the candidate is simply converting the decimal number 23 in a binary number:

2310 = 111012 = [Yes, Yes, Yes, No, Yes], where Yes=1 and No=0

Each card shows all the numbers with the same binary-digit set to 1.

The quiz-master computes the reconversion to decimal by calculating the base-polynomial:

1 x 24 + 0 x 23 + 1 x 22 + 1 x 21 + 1 x 20

= 1 x 16 + 0 x 8 + 1 x 4 + 1 x 2 + 1 x 1 = 23

In fact CORDIC-algorithms are based on this sort of computing. The interest is of course the proximity of the binary-system to computer-systems. Multiplying by 2 is equivalent of shifting the binary number 1 digit to the left. Dividing by 2 is the same as rotating 1 digit to the right:

111012 x 210 = 1110102

111012 DIV 210 = 1110.12

These shift-operations are extremely quick.

NOTE: in only one of our examples this shift-trick is used, for only few higher computer-languages allow access to these low-level functions. But CORDIC has another speed-advantage which comes from the exponential approach. Multiplying and dividing may be reduced to additions and substractions.

To compute a square-root with CORDIC the number is yielded by multiplying, adding and testing. 

L

2^L

y

x=

 12056
    0

initial value

  
7 128 0 128 x 128 > 12056 do nothing
6 64 64 64 x 64 < 12056 add 64 to yinitial --> 64
5 32 96 (64 + 32)2 < 12056 add 32 to last y --> 96
4 16 96 (96 + 16)2 > 12056

do nothing
3 8 104 (96 + 8)2 < 12056 add 8 to last y --> 104
2 4 108 (104 + 4)2 < 12056 add 4 to last y --> 108
1 2 108 (108 + 2)2 > 12056

do nothing
0 1 109 (108 + 1)2 < 12056 add 1 to last y --> 109
-1 0.5 a.s.o. and so on

 and so on

Here a C-routine for integer-square-rooting for numbers between 0 and 65536:

  • int sqrt (int x)
  • {
  • int base, i, y ;
  •        base = 128 ;
  •        y = 0 ;
  •        for (i = 1; i <= 8; i++)
  •        {
  •                y + =  base ;
  •                if  ( (y * y) > x )
  •                {
  •                        y -= base ;  // base should not have been added, so we substract again
  •                }
  •                base >> 1 ;      // shift 1 digit to the right = divide by 2
  •         }
  •         return y ;
  • }

Here a Robolab-version: (you may use our text-based modifiers or use the variable numbers of your choice)

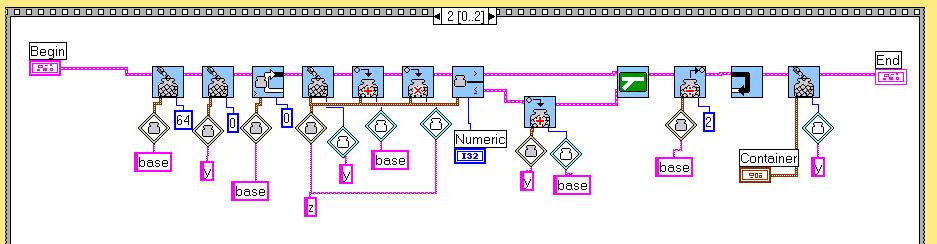
One computation needs about 0.2 seconds. 

Here a test-program:

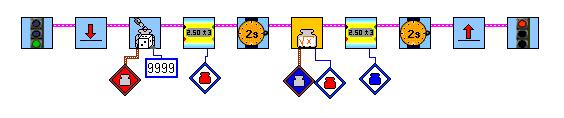
The program continuously shows a random number and its integer square-root.

RetourMain Page