Tower_of_Hanoi

Tower of Hanoi

The robot which we are refering to here is the Hanoi-Solver from JP Brown.

We found this picture in a marvelous German book about puzzles "Schöne Spiele", Walter Sperling, Recklinghausen, 1954, p. 141

The author tells the story about Asian monks, occupied for thousands of years with the problem of the Tower of Hanoi. Generations ever since were busy at work to transfer wooden discs from one place to another respecting some rules :

There are only three places where the discs may be stacked
At start, all the discs are stacked by descending radius at implacement A
The work is finished when all the discs are stacked in place C in correct order
Only one disc may be moved at a time
No larger disc may be deposited onto a smaller one

The more discs there are, the more movements have to be done. Mathematicians have tried to find out the minimum of movements for a given set of discs. Computer scientists have developped many algorithms to solve the problem.

LEGO specialist J. BROWN proposes a remarkable robot-solution. With his program the robot may solve the problem for discs 1 through 5. The program was written in nqc (firmware 2.0) and uses a non-recursive algorithm.

(photo: copyright JP Brown)

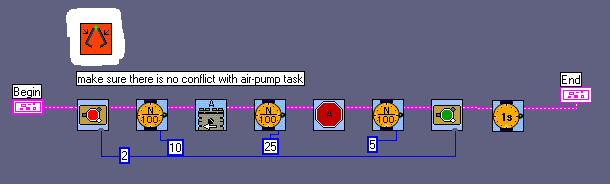
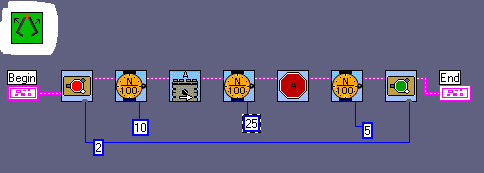
We tried to design a ROBOLAB-program for it. As such a program must handle variables, ROBOLAB is perhaps not the best choice. But with the creating sub.vis feature, those programs are better readable than text-orientated ones.

First we chose to program the Tower of Hanoi in Delphi to illustrate the power - and the limitations - of RECURSIVE PROGRAMS. This means that the main algorithm is caracterised by a procedure that calls itself top solve the given problem. DOWNLOAD TOWER OF HANOI

procedure TForm1.Button1Click(Sender: TObject);
        procedure move(source,destn,spare,n:integer);
        begin
             if n>1 then move(source,spare,destn,n-1); //The procedure calls itself !!
             richedit1.lines.add(inttostr(richedit1.lines.count)+'. Moving from '+
                                              inttostr(source)+ ' to '+inttostr(destn));
             if n>1 then move(spare,destn,source,n-1); //The procedure calls itself !!
        end;
begin //Main program part
      richedit1.clear;
      richedit1.Lines.add(edit1.text+' discs');
      move(1,3,2,strToint(edit1.text));
end;

If you download this program, try different number of discs, but be aware: if you don't have a CRAY- supercomputer, do not try more than 20 discs !! For a Pentium III at 1GHz this will take several hours of computations. The power of recursive algorithms is the extreme shortness of program-code. The limitation is the blowing-up of memory-use and computer-time.

More information about the Tower of Hanoi problem and its solutions.

Our ROBOLAB-functions: DOWNLOAD ALL THE FILES

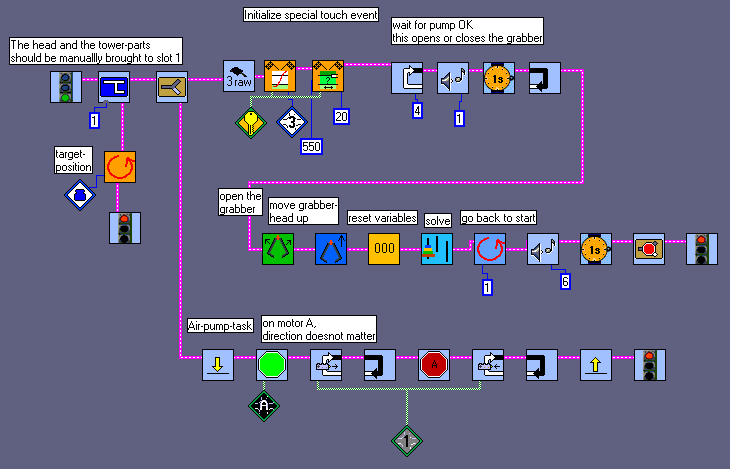
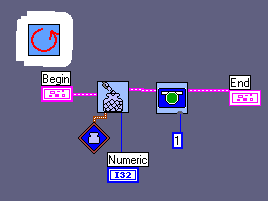
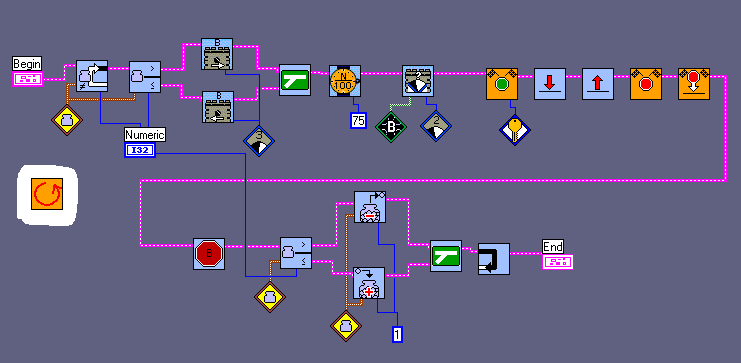
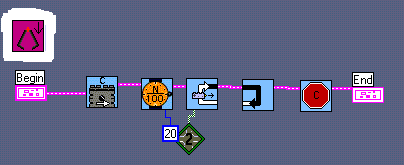
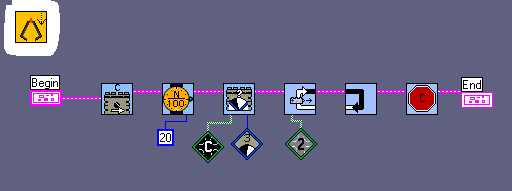
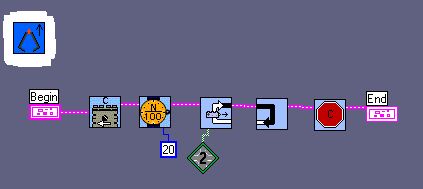
and two special sub.vis :

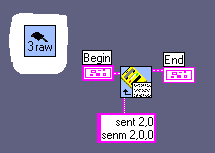
You may be disappointed that the program does not have any own Tower of Hanoi - algorithm. In fact our program may solve the two, three and four discs problem with different variable-values. But the movement-commands have to be stored. The RCX does not solve the problem itself, it only executes the movements.

Notes:

JP Brown's Hanoi-robot does not always stop correctly at the peg-position. To overcome this we had to change the trigger-values of the implicated touch-sensor. This was done using the event-monitoring feature of Robolab 2.5. (Note that the event-monitoring gives a quicker reaction to events than the traditional wait-until function !)
For the first time we are using the indirect addressing feature of the firmware 2.0. In Robolab this is called container's container.
The movements are coded by pairs: (have a look at the O O O - sub.vi)
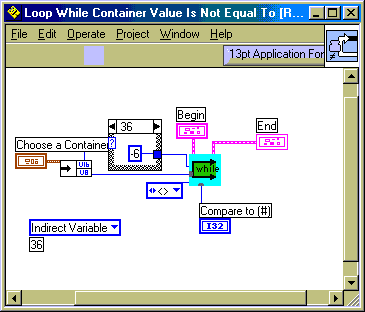
Starting at variable 4 we set the variables for the movements:
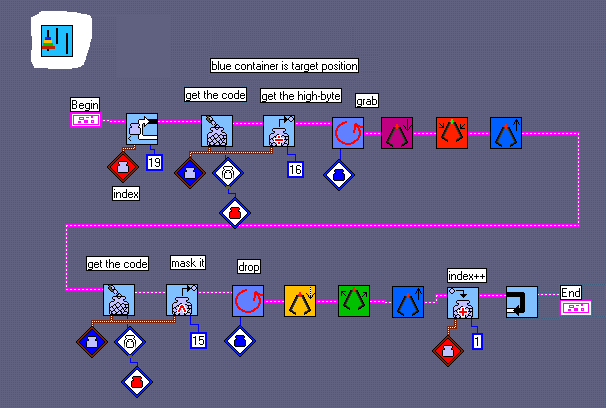
- set 0,4,2,18 which means set variable 4 to constant value 18
- 18 is the hexadecimal 0x12 - you recognize move 1 to 2
- to extract the starting (grab) place we divide 18 by 16 e.a. 1
- to explain the extraction of the ending point (drop), we must have a look at the binary representation of 18 which is b0001 0010 . We mask the high-byte by operating the bitwise AND-function with the number b0000 1111. Thus we obtain b0000 0010 which is the value 2
We had to operate some technical improvements of the robot which you can find in the download zip-file.
At no time the robot worked only with batteries. We had to run it using the AC-adapter. The major problem is the weak torque and important friction of the chain-system.

Main Page