![]()
How to build recursive functions
Ultimate Robolab allows the use of recursive functions. For those not being familiar with the expression "recursive function", let's propose the following definition :
Imagine that you want to program your RCX to compute the sum of all the numbers from 1 to 100. In fact, it is reported that one of the greatest mathematicians of all the times, Carl Friedrich Gauss, was imposed this exercise by his teacher, when he was an eight year old boy. He found a well-known short-hand solution. He wrote down the numbers to a list in ascending and in descending order. He then added the list items by couples from the bottom to the top, recognizing that the small sums always were identical (=101) :
| 1 | 2 | 3 | 4 | .... | 97 | 98 | 99 | 100 + |
| 100 | 99 | 98 | 97 | .... | 4 | 3 | 2 | 1 |
| 101 | 101 | 101 | 101 | .... | 101 | 101 | 101 | 101 |
S = 101 * 100 / 2 = 5050 (divide by two, because the numbers all are counted twice)
It is easy to prove the general formula: Sn = 1+2+3+4+...+n = (n+1) * n / 2 by induction :
I0: S0 = 1 * 0 / 2 = 0
In: we suppose the hypothesis to be true for n: Sn = (n+1) * n / 2, let's prove it for n+1 :
| In+1: Sn+1 | = (n+1) + Sn |
| = (n+1) + (n+1) * n / 2 | |
| = (n+1) * 2 / 2 + (n+1) * n / 2 | |
| = (n+1) * (2+n) / 2, because of distributivity | |
| = (n+2) * (n+1) / 2, because of commutativity | |
| confirming the truth of the hypothesis |
1. Iterative solution
Gauss's less intelligent class-collegues did the operation slowly by making successive additions:
1 + 2 = 3
3 + 3 = 6
6 + 4 = 10 ....
These painful and time-intensive calculations also yield the correct result, but.... With Ultimate Robolab you could program your RCX to do those computations as follows:
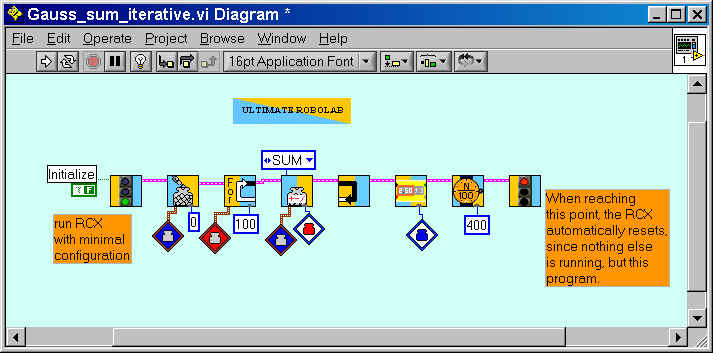
or better by calling a function denominated "Sum" doing exactly the same, with the only difference to be using so-called "stack-variables". (These will be introduced at another page.)
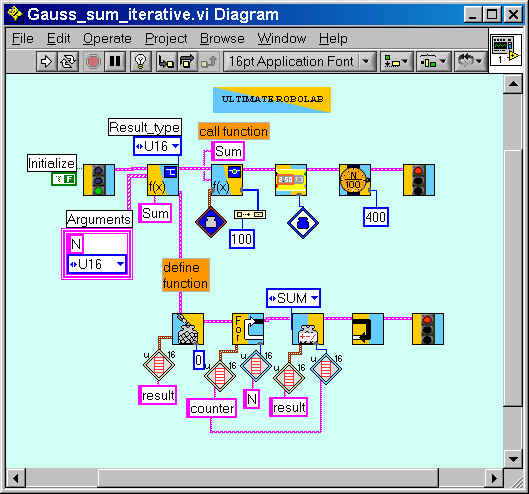
2. Recursive solution
However you could look at the function differently:
S100 = 100 + S99
S99 = 99 + S98
S98 = 98 + S97
....
S1 = 1 + S0
S0 = 0
This means that if you can solve the problem for N=100 by solving it for N-1=99. This one can be solved by doing it for N-2=98 and so on, until you reach the so-called termination condition.
Gauss' exercise may be considered as an example of a recursive function.
For various reasons it is far from being obvious to have computers being able to operate such functions.
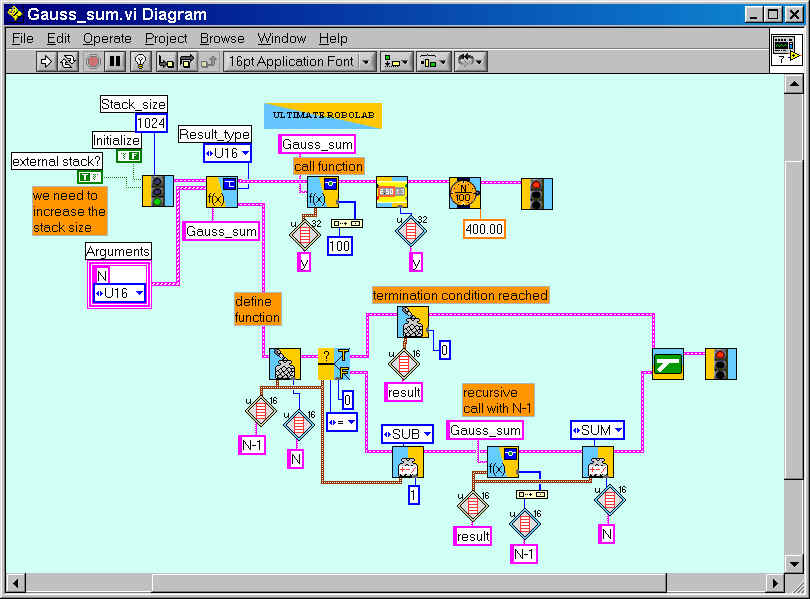
Note that the size of the "stack" has to be increased here. (The stack will be explained at another page.)
The interest in recursive functions does not appear in this example. But, imagine that you want to compute the factorial function, which instead of doing the sum of all consecutive numbers, operates the multiplying. There doesn't exist any short-hand formula for this function, so the problem can only be solved either iteratively or recursively.
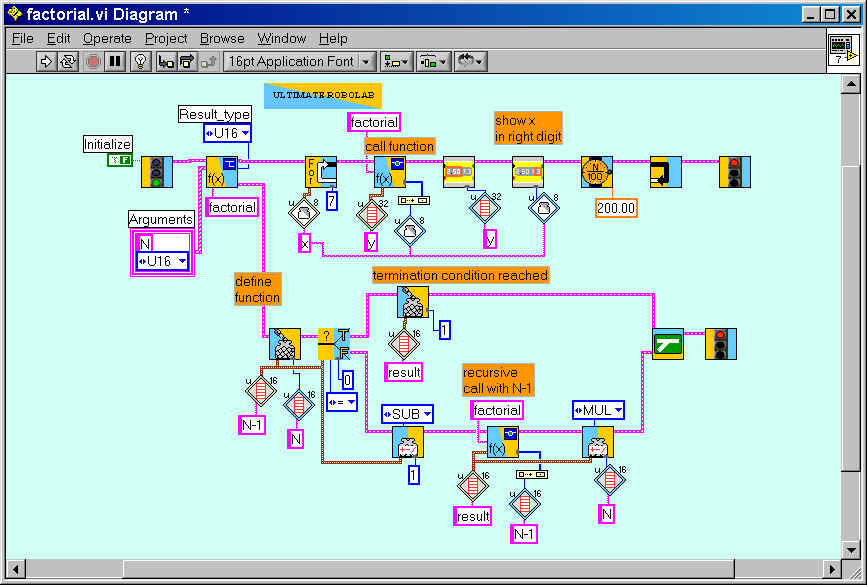
Recursive functions normally are used to solve search or sorting problems, where they are much more efficient and fast than any other algorithm. This will be shown at another page.